Chapter 7, part 3 of 6: binomial trees
Welcome back.
This week, part 3 of the series on the QuantLib tree framework that started a couple of posts ago. But first, do you see anything different in the address bar?
Yes, this blog has its own domain now. It’s at http://implementingquantlib.com. It’s not that different, of course, but it’s easier to remember (and it might make it possible in future to switch to other blogging options without inconveniencing you, dear reader). You don’t need to change your bookmarks or your feeds right away: the old address is still working and is being redirected to the new one.
Follow me on Twitter if you want to be notified of new posts, or add me to your circles, or subscribe via RSS: the buttons for that are in the footer. Also, make sure to check my Training page.
Trees and tree-based lattices
In order to use the assets I described in the previous post, we need a lattice. The first question we have to face is at the very beginning of its design: should the tree itself be the lattice, or should we have a separate lattice class using a tree?
Even if the first alternative can be argued (a tree can very well be seen as a kind of lattice, so an is-a relationship would be justified), the library currently implements the second. I’m afraid the reasons for the choice are lost in time; one might be that having a class for the lattice and one for the tree allows us to separate different concerns. The tree has the responsibility for maintaining the structure and the probability transitions between nodes; the lattice uses the tree structure to roll the asset back and adds some additional features such as discounting.
The Tree class template
As I just wrote, a tree provides information about its structure. It can be described by the number of nodes at each level (each level corresponding to a different time), the nodes that can be reached from each other node at the previous level, and the probabilities for each such transition.
The interface chosen to represent this information (shown in the
listing below) was an index-based one. Nodes were not represented as
instances of a Node class or structure; instead, the tree was
described—not implemented, mind you—as a series of vectors
of increasing size, and the nodes were identified by their indexes
into the vectors. This gives more flexibility in implementing
different trees; one tree class might store the actual vectors of
nodes, while another might just calculate the required indexes as
needed. In the library, trinomial trees are implemented in the first
way and binomial trees in the second. I’ll describe both later on.
class Tree {
public:
Tree(Size columns);
virtual ~Tree();
Size columns() const;
virtual Size size(Size i) const = 0;
virtual Real underlying(Size i, Size j) const = 0;
virtual Size branches() const = 0;
virtual Size descendant(Size i, Size j,
Size branch) const = 0;
virtual Real probability(Size i, Size index,
Size branch) const = 0;
};The methods shown in the interface fully describe the tree
structure. The columns method returns the number of levels in the
tree; evidently, the original designer visualized the time axis as
going from left to right, with the tree growing in the same
direction. If we were to change the interface, I’d probably go for a
more neutral name, such as size.
The size name was actually taken for another method, which returns
the number of nodes at the i-th level of the tree; the underlying
method takes two indexes i and j and returns the value of the variable
underlying the tree at the j-th node of the i-th level.
The remaining methods deal with branching. The branches method
returns the number of branches for each node (2 for binomial trees, 3
for trinomial ones and so on). It takes no arguments, which means that
we’re assuming such a number to be constant; we’ll have no trees with
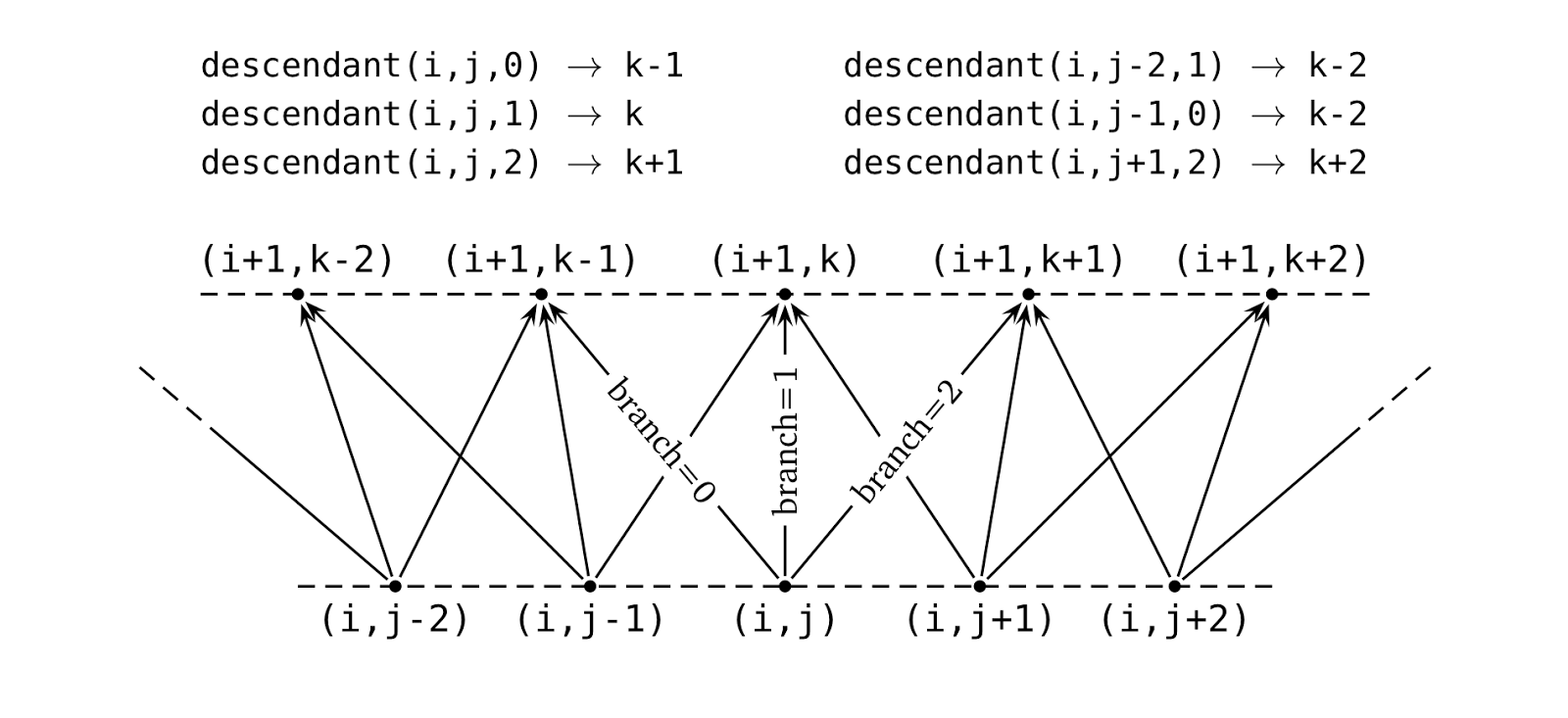
a variable number of branches. The descendant identifies the nodes
towards which a given node is branching: it takes the index i of the
level, the index j of the node and the index of a branch, and returns
the index of the corresponding node on level i+1 as exemplified in the
following figure. Finally, the probability method takes the same
arguments and returns the probability to follow a given branch.
The original implementation actually sported a base Tree class as
shown in the listing above. It worked, but it committed what amounts
to a mortal sin in numerical code: it declared as virtual some methods
(such as descendant or probability) that were meant to be called
thousands of times inside tight nested loops. (If you’re wondering why
this is bad, see for instance [1] for a short explanation—along
with a lot more information on using C++ for numerical work.) After a
while, we started to notice that small glaciers were disappearing in
the time it took us to calibrate a short-rate model.
Eventually, this led to a reimplementation. We used the Curiously
Recurring Template Pattern (CRTP) to replace run-time with
compile-time polymorphism (see the aside below if you need a
refresher) which led to the Tree class template shown in the next
listing. The virtual methods are gone, and only the non-virtual
columns method remains; the machinery for the pattern is provided by
the CuriouslyRecurringTemplate class template, which avoids
repetition of boilerplate code by implementing the const and
non-const versions of the impl method used in the pattern.
template <class T>
class Tree : public CuriouslyRecurringTemplate<T> {
public:
Tree(Size columns) : columns_(columns) {}
Size columns() const { return columns_; }
private:
Size columns_;
};This was not a redesign; the existing class hierarchy was left unchanged. Switching to CRTP yielded slightly more complex code, as you’ll see when I describe binomial and trinomial trees. However, it paid off in speed: with the new implementation, we saw the performance increase up to 10x. Seeing the results, I didn’t stop to ask myself many question (yes, I’m the guilty party here) and I missed an opportunity to simplify the code. With a cooler head, I might have noticed that the base tree classes don’t call methods defined in derived classes, so I could have simplified the code further by dropping CRTP for simple templates. (If a new branch of the hierarchy were to need CRTP, it could be added locally to that branch.) Yet another thing to remember when we decide to redesign parts of the library.
Aside: curiouser and curiouser.
The Curiously Recurring Template Pattern (CRTP) was named and popularized by James Coplien in 1995 [2] but it predates his description. It is a way to achieve a static version of the Template Method pattern (see [3], of course), in which a base class implements common behavior and provides hooks for customization by calling methods that will be implemented in derived classes.
The idea is the following:
template <T>
class Base {
public:
T& impl() {
return static_cast<T&>(*this);
}
void foo() {
...
this->impl().bar();
...
}
};
class Derived : public Base<Derived> {
public:
void bar() { ... }
};Now if we instantiate a Derived and call its foo method, it will
in turn call the correct bar implementation: that is, the one
defined in Derived (note that Base doesn’t declare bar at all).
We can see how this work by working out the expansion made by the
compiler. The Derived class doesn’t define a foo method, so it
inherits it from the its base class; that is, Base<Derived>. The
foo method calls impl, which casts *this to a reference to the
template argument T, i.e., Derived itself. We called the method on
a Derived instance to begin with, so the cast succeeds and we’re
left with a reference to our object that has the correct type. At this
point, the compiler resolves the call to bar on the reference to
Derived::bar and thus the correct method is called. All this happens
at compile time, and enables the compiler to inline the call to bar
g and perform any optimization it sees fit.
Why go through all this, and not just call bar from foo instead?
Well, it just wouldn’t work. If we didn’t declare bar into Base,
the compiler wouldn’t know what method we’re talking about; and if we
did declare it, the compiler would always resolve the call to the
Base version of the method. CRTP gives us a way out: we can define
the method in the derived class and use the template argument to pass
its type to the base class so that the static cast can close the
circle.
Binomial trees
As I mentioned earlier, a tree might implement its required interface
by storing actual nodes or by just calculating their indexes on
demand. The BinomialTree class template, shown in the listing below,
takes the second approach. In a way, the nodes are the indexes; they
don’t exist as separate entities.
template <class T>
class BinomialTree : public Tree<T> {
public:
enum Branches { branches = 2 };
BinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps)
: Tree<T>(steps+1) {
x0_ = process->x0();
dt_ = end/steps;
driftPerStep_ = process->drift(0.0, x0_) * dt_;
}
Size size(Size i) const {
return i+1;
}
Size descendant(Size, Size index, Size branch) const {
return index + branch;
}
protected:
Real x0_, driftPerStep_;
Time dt_;
};The class template models a rather strict subset of the possible binomial trees, that is, recombining trees with constant drift and diffusion for the underlying variable and with constant time steps. (The library contains, in its ``experimental’’ folder, an extension of this class to non-constant parameters; you’re welcome to have a look at it and send us feedback. For illustration purposes, though, I’ll stick to the constant version here.)
Even with these constraints, there’s quite a few different
possibilities for the construction of the tree, so most of the
implementation is left to derived classes. This class acts as a base
and provides the common facilities; first of all, a branches
enumeration whose value is defined to be 2 and which replaces the
corresponding method in the old Tree class. Nowadays, we’d use a
static const Size data member for the purpose; the enumeration is a
historical artifact from a time when compilers were less
standard-compliant.
The class constructor takes a one-dimensional stochastic process
providing the dynamics of the underlying, the end time of the tree
(with the start time assumed to be \( 0 \), another implicit
constraint), and the number of time steps. It calculates and stores a
few simple quantities: the initial value of the underlying, obtained
by calling the x0 method of the process; the size of a time step,
obtained by dividing the total time by the number of steps; and the
amount of underlying drift per step, once again provided by the
process (since the parameters are constant, the drift is calculated at
\( t=0 \)). The class declares corresponding data members for each
of these quantities.
Unfortunately, there’s no way to check that the given process is actually one with constant parameters. On the one hand, the library doesn’t declare a specific type for that kind of process; it would be orthogonal to the declaration of different process classes, and it would lead to multiple inheritance—the bad kind—if one wanted to define, say, a constant-parameter Black-Scholes process (it would have to be both a constant-parameter process and a Black-Scholes process). Therefore, we can’t enforce the property by restricting the type to be passed to the constructor. On the other hand, we can’t write run-time tests for that: we might check a few sample points, but there’s no guarantee that the parameters don’t change elsewhere.
One option that remains is to document the behavior and trust the user not to abuse the class. Another (which we won’t pursue now for backward compatibility, but might be for a future version of the library) would be for the constructor to forgo the process and take the constant parameters instead. However, this would give the user the duty to extract the parameters from the process at each constructor invocation. As usual, we’ll have to find some kind of balance.
The two last methods define the structure of the tree. The size
method returns the number of nodes at the \( i \)-th level; the code
assumes that there’s a single node (the root of the tree) at level \(
0 \), which gives \( i+1 \) nodes at level \( i \) because of
recombination. This seems reasonable enough, until we realize that we
also assumed that the tree starts at \( t=0 \). Put together, these
two assumptions prevent us from implementing techniques such as, say,
having three nodes at \( t=0 \) in order to calculate Delta and
Gamma by finite differences. Luckily enough, this problem might be
overcome without losing backward compatibility: if one were to try
implementing it, the technique could be enabled by adding additional
constructors to the tree, thus allowing to relax the assumption about
the start time.
Finally, the descendant method describes the links between the
nodes. Due to the simple recombining structure of the tree, the node
at index \( 0 \) on one level connects to the two nodes at index \(
0 \) and \( 1 \) on the next level, the node at index \( 1 \) to
those at index \( 1 \) and \( 2 \), and in general the node at
index \( i \) to those at index \( i \) and \( i+1 \). Since the
chosen branch is passed as an index (\( 0 \) or \( 1 \) for a
binomial tree) the method just has to add the index of the node to
that of the branch to return the correct result. Neither index is
range-checked, since the method will be called almost always inside a
loop; checks would not only be costly (which is possible, but I
haven’t measured the effect, so I’ll leave it at that) but actually
redundant, since they will already be performed while setting up the
loop.
The implementation of the BinomialTree class template misses the
methods that map the dynamics of the underlying to the tree nodes:
that is, the underlying and probability methods. They are left to
derived classes, since there are several ways in which they can be
written. In fact, there are families of ways: the two class templates
in the following listing are meant to be base classes for two such
families.
template <class T>
class EqualProbabilitiesBinomialTree : public BinomialTree<T> {
public:
EqualProbabilitiesBinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end,
Size steps)
: BinomialTree<T>(process, end, steps) {}
Real underlying(Size i, Size index) const {
int j = 2*int(index) - int(i);
return this->x0_*std::exp(i*this->driftPerStep_
+ j*this->up_);
}
Real probability(Size, Size, Size) const {
return 0.5;
}
protected:
Real up_;
};
template <class T>
class EqualJumpsBinomialTree : public BinomialTree<T> {
public:
EqualJumpsBinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end,
Size steps)
: BinomialTree<T>(process, end, steps) {}
Real underlying(Size i, Size index) const {
int j = 2*int(index) - int(i);
return this->x0_*std::exp(j*this->dx_);
}
Real probability(Size, Size, Size branch) const {
return (branch == 1 ? pu_ : pd_);
}
protected:
Real dx_, pu_, pd_;
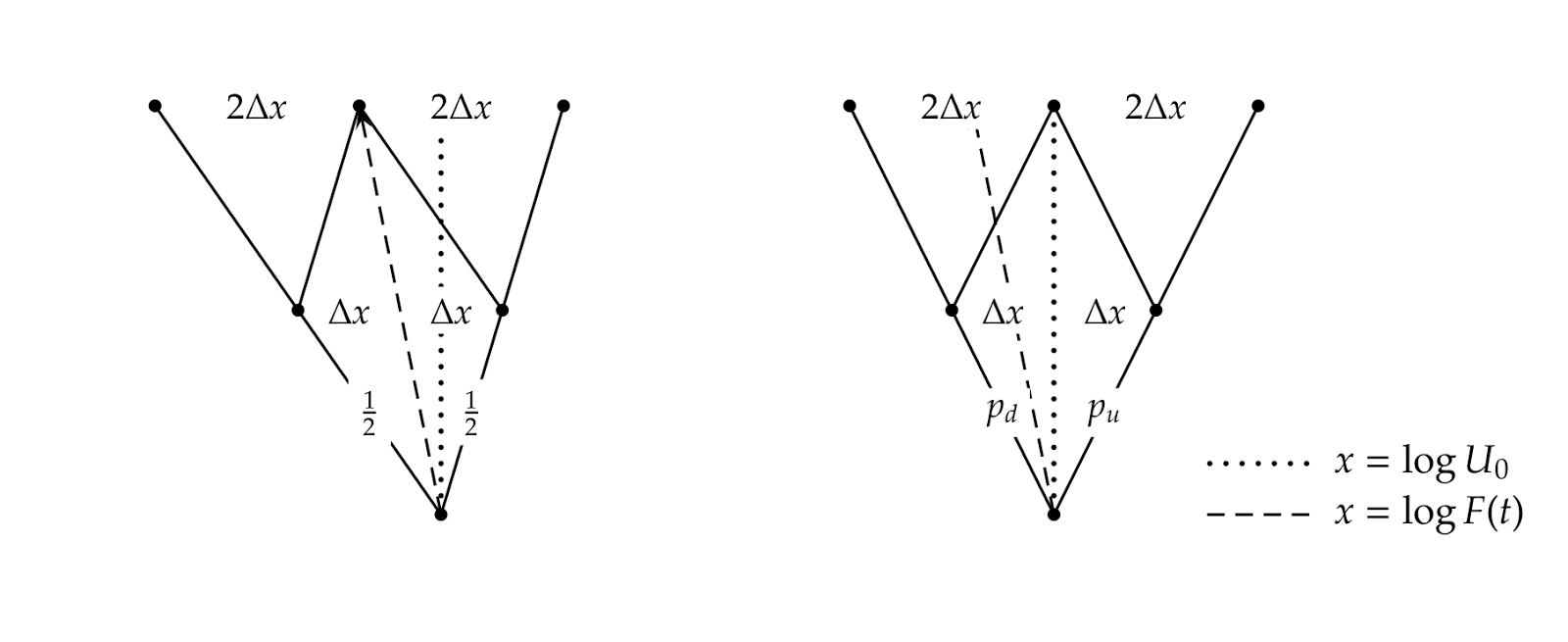
};The first, EqualProbabilitiesBinomialTree, can be used for those
trees in which from each node there’s the same probability to go to
either branch. This obviously fixes the implementation of the
probability method, which identically returns 1/2, but also sets
constraints on the underlying method. Equal probability to go along
each branch means that the spine of the tree (that is, the center
nodes of each level) is the expected place to be; and in turn, this
means that such nodes must be placed at the forward value of the
underlying for the corresponding time (see the figure below for an
illustration of the idea). The class defines an underlying method
that implements the resulting formula for the logarithm of the
underlying (you can tell that the whole thing was written with the
Black-Scholes process in mind). A data member up_ is defined and
used to hold the half-displacement from the forward value per each
move away from the center, represented by \( \Delta x \) in the
figure; however, the constructor of the class does not give it a
value, leaving this small freedom to derived classes.
The second template, EqualJumpsBinomialTree, is used for those trees
in which going to either branch implies an equal amount of movement in
opposite directions for the logarithm of the underlying (again, see
the figure below); since one of the directions goes with the drift and
the other against it, the probabilities are different. The template
defines the underlying method accordingly, leaving to derived
classes the task of filling the value of the dx_ data member; and it
also provides an implementation for the probability method that
returns one of two values (pu_ or pd_) which must also be
specified by derived classes.
Finally, the three classes in the following listing are examples of
actual binomial trees, and as such are no longer class templates. The
first implements the Jarrow-Rudd tree; it inherits from
EqualProbabilitiesBinomialTree (note the application of CRTP) and
its constructor sets the up_ data member to the required value,
namely, the standard deviation of the underlying distribution after
one time step. The second implements the Cox-Ross-Rubinstein tree,
inherits from EqualJumpsBinomialTree, and its constructor calculates
the required probabilities as well as the displacement. The third one
implements the Tian tree, and provides an example of a class that
doesn’t belong to either family; as such, it inherits from
BinomialTree directly and provides all required methods.
class JarrowRudd
: public EqualProbabilitiesBinomialTree<JarrowRudd> {
public:
JarrowRudd(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: EqualProbabilitiesBinomialTree<JarrowRudd>(process,
end, steps) {
up_ = process->stdDeviation(0.0, x0_, dt_);
}
};
class CoxRossRubinstein
: public EqualJumpsBinomialTree<CoxRossRubinstein> {
public:
CoxRossRubinstein(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: EqualJumpsBinomialTree<CoxRossRubinstein>(process,
end, steps) {
dx_ = process->stdDeviation(0.0, x0_, dt_);
pu_ = 0.5 + 0.5*driftPerStep_/dx_;
pd_ = 1.0 - pu_;
}
};
class Tian : public BinomialTree<Tian> {
public:
Tian(const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: BinomialTree<Tian>(process, end, steps) {
// sets up_, down_, pu_, and pd_
}
Real underlying(Size i, Size index) const {
return x0_ * std::pow(down_, Real(int(i)-int(index)))
* std::pow(up_, Real(index));
};
Real probability(Size, Size, Size branch) const {
return (branch == 1 ? pu_ : pd_);
}
protected:
Real up_, down_, pu_, pd_;
};Bibliography
[1] T. Veldhuizen, Techniques for Scientific
C++. Indiana
University Computer Science Technical Report TR542.
[2] J.O. Coplien, A Curiously Recurring Template Pattern. In
S.B. Lippman, editor, C++ Gems. Cambridge University Press, 1996.
[3] E. Gamma, R. Helm, R. Johnson and J. Vlissides, Design Patterns:
Element of Reusable Object-Oriented Software. Addison-Wesley, 1995.