Chapter 7, part 1 of 6: the tree framework
Welcome back.
This week, some content from my book (which, as I announced last week, is now available as an ebook from Leanpub; thanks to all those who bought it so far). This post is the first part of a series that will describe the QuantLib tree framework.
But first, some news: with the help and organization of the good Jacob Bettany from MoneyScience, I’ll hold a new edition of my Introduction to QuantLib Development course. It’s an intensive three-day course in which I explain the architecture of the library and guide attendees through exercises that let them build new financial instruments based on the frameworks I describe. It will be in London from June 29th to July 1st, and you can find more info and a brochure at this link. An early-bird discount is available until April 30th.
Subscribe to my Substack to receive my posts in your inbox, or follow me on Twitter or LinkedIn if you want to be notified of new posts, or subscribe via RSS if you’re the tech type: the buttons for all that are in the footer. Also, I’m available for training, both online and (when possible) on-site: visit my Training page for more information.
The tree framework
Together with Monte Carlo simulations, trees are among the most commonly used tools in quantitative finance. As usual, the dual challenge for a framework is to implement a number of reusable (and possibly composable) pieces and to provide customization hooks for injecting new behavior. The QuantLib tree framework has gone through a few revisions, and the current version is a combination of object-oriented and generic programming that does the job without losing too much performance in the process.
The Lattice and DiscretizedAsset classes
The two main classes of the framework are the Lattice and
DiscretizedAsset classes. In our intentions, the Lattice class
(shown in the listing below) was to model the generic concept of a
discrete lattice, which might have been a tree as well as a
finite-difference grid. This never happened; the finite-difference
framework went its separate way and is unlikely to come back any time
soon. However, the initial design helped keeping the Lattice class
clean: to this day, it contains almost no implementation details and
is not tied to trees.
class Lattice {
public:
Lattice(const TimeGrid& timeGrid) : t_(timeGrid) {}
virtual ~Lattice() {}
const TimeGrid& timeGrid() const { return t_; }
virtual void initialize(DiscretizedAsset&,
Time time) const = 0;
virtual void rollback(DiscretizedAsset&,
Time to) const = 0;
virtual void partialRollback(DiscretizedAsset&,
Time to) const = 0;
virtual Real presentValue(DiscretizedAsset&) const = 0;
virtual Disposable<Array> grid(Time) const = 0;
protected:
TimeGrid t_;
};Its constructor takes a TimeGrid instance and stores it (its only
concession to implementation inheritance, together with an inspector
that returns the time grid). All other methods are pure virtual. The
initialize method must set up a discretized asset so that it can be
put on the lattice at a given time. (I do realize this is mostly
hand-waving right now. It will become clear as soon as we get to a
concrete lattice.) The rollback and partialRollback methods roll
the asset backwards in time on the lattice down to the desired time
(with a difference I’ll explain later); and the presentValue method
returns what its name says.
Finally, the grid method returns the values of the discretized
quantity underlying the lattice. This is a bit of a smell. The
information was required in other parts of the library, and we didn’t
have any better solution. However, this method has obvious
shortcomings. On the one hand, it constrains the return type, which
either leaks implementation or forces a type conversion; and on the
other hand, it simply makes no sense when the lattice has more than
one factor, since the grid should be a matrix or a cube in that
case. In fact, two-factor lattices implement it by having it throw an
exception. All in all, this method is up for some serious improvement
in future versions of the library.
The DiscretizedAsset class is the base class for the other side of
the tree framework—the Costello to Lattice’s Abbott, as it
were. It models an asset that can be priced on a lattice: it works
hand in hand with the Lattice class to provide generic behavior, and
has hooks that derived classes can use to add behavior specific to the
instrument they implement.
As can be seen from the listing below, it’s not nearly as abstract as
the Lattice class. Most of its methods are concrete, with a few
virtual ones that use the Template Method pattern to inject behavior.
class DiscretizedAsset {
public:
DiscretizedAsset()
: latestPreAdjustment_(QL_MAX_REAL),
latestPostAdjustment_(QL_MAX_REAL) {}
virtual ~DiscretizedAsset() {}
Time time() const { return time_; }
Time& time() { return time_; }
const Array& values() const { return values_; }
Array& values() { return values_; }
const shared_ptr<Lattice>& method() const {
return method_;
}
void initialize(const shared_ptr<Lattice>&,
Time t) {
method_ = method;
method_->initialize(*this, t);
}
void rollback(Time to) {
method_->rollback(*this, to);
}
void partialRollback(Time to) {
method_->partialRollback(*this, to);
}
Real presentValue() {
return method_->presentValue(*this);
}
virtual void reset(Size size) = 0;
void preAdjustValues() {
if (!close_enough(time(),latestPreAdjustment_)) {
preAdjustValuesImpl();
latestPreAdjustment_ = time();
}
}
void postAdjustValues() {
if (!close_enough(time(),latestPostAdjustment_)) {
postAdjustValuesImpl();
latestPostAdjustment_ = time();
}
}
void adjustValues() {
preAdjustValues();
postAdjustValues();
}
virtual std::vector<Time> mandatoryTimes() const = 0;
protected:
bool isOnTime(Time t) const {
const TimeGrid& grid = method()->timeGrid();
return close_enough(grid[grid.index(t)],time());
}
virtual void preAdjustValuesImpl() {}
virtual void postAdjustValuesImpl() {}
Time time_;
Time latestPreAdjustment_, latestPostAdjustment_;
Array values_;
private:
shared_ptr<Lattice> method_;
};Its constructor takes no argument, but initializes a couple of internal variables. The main inspectors return the data comprising its state, namely, the time \( t \) of the lattice nodes currently occupied by the asset and its values on the same nodes; both inspectors give both read and write access to the data to allow the lattice implementation to modify them. A read-only inspector returns the lattice on which the asset is being priced.
The next bunch of methods implements the common behavior that is inherited by derived classes and provide the interface to be called by client code. The body of a tree-based engine will usually contain something like the following after instantiating the tree and the discretized asset:
asset.initialize(lattice, T);
asset.rollback(t0);
results_.value = asset.presentValue();The initialize method stores the lattice that will be used for
pricing and sets the initial values of the asset (or rather its final
values, since the time T passed at initialization is the maturity
time); the rollback method rolls the asset backwards on the lattice
until the time t0; and the presentValue method extracts the value
of the asset as a single number.
The three method calls above seem simple, but their implementation
triggers a good deal of behavior in both the asset and the lattice and
involves most of the other methods of DiscretizedAsset as well as
those of Lattice. The interplay between the two classes is not
nearly as funny as Who’s on First, but it’s almost as complex to
follow; thus, you might want to refer to the sequence diagram shown
below.
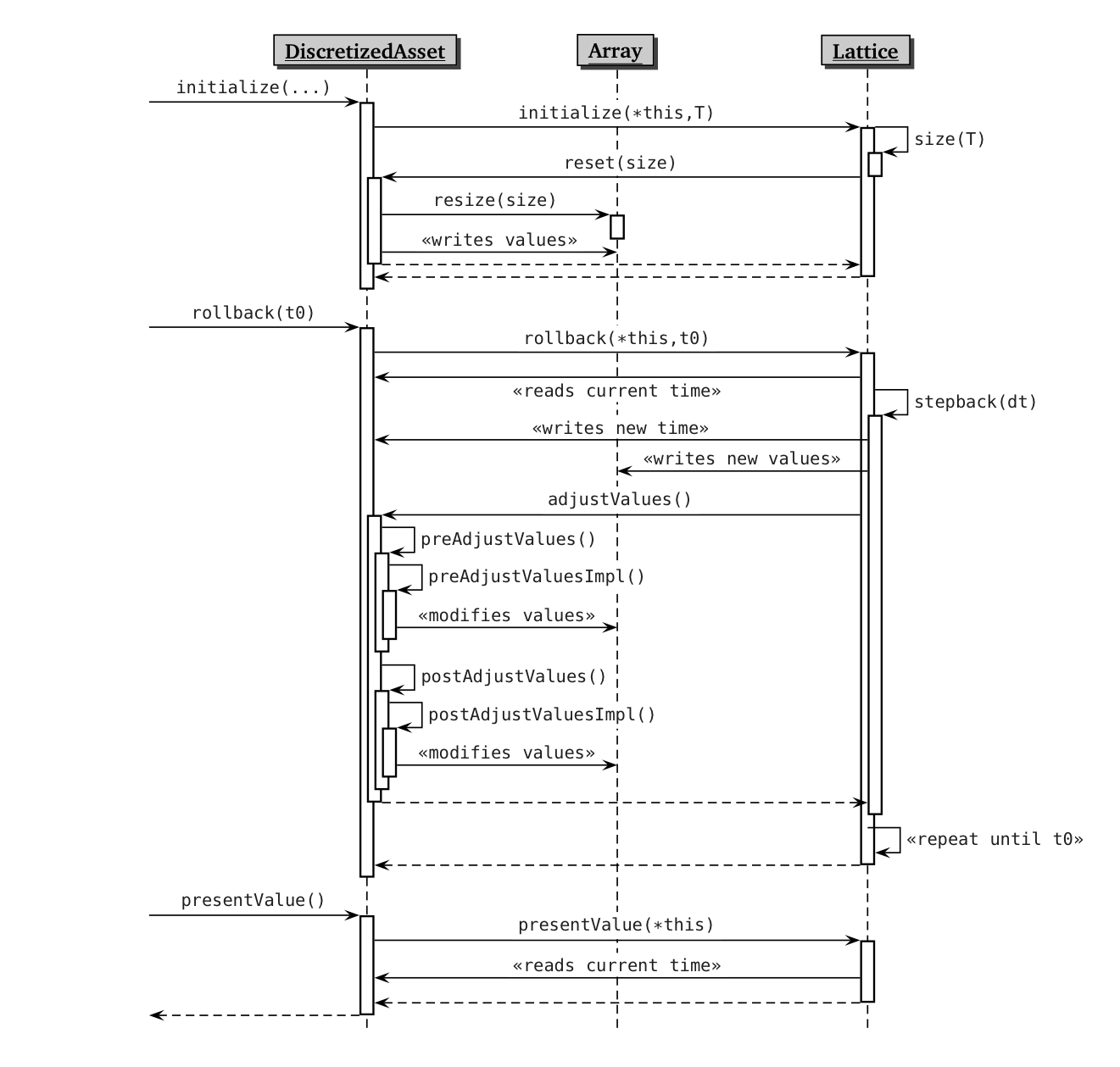
The initialize method sets the calculation up by placing the asset
on the lattice at its maturity time (the asset’s, I mean) and
preparing it for rollback. This means that on the one hand, the vector
holding the asset values on each lattice node must be dimensioned
correctly; and on the other hand, that it must be filled with the
correct values. Like most of the DiscretizedAsset methods,
initialize does this by delegating part of the actual work to the
passed lattice; after storing it in the corresponding data member, it
simply calls the lattice’s initialize method passing the maturity
time and the asset itself.
Now, the Lattice class doesn’t implement initialize, which is left
as purely virtual; but any sensible implementation in derived classes
will do the dance shown in the sequence diagram. It might perform some
housekeeping step of its own, not shown here; but first, it will
determine the size of the lattice at the maturity time (that is, the
number of nodes) probably by calling a corresponding method; then, it
will store the time into the asset (as you remember, the asset
provides read/write access to its state) and pass the size to the
asset’s reset method. The latter, implemented in derived classes,
will resize the vector of values accordingly and fill it with
instrument-specific values (for instance, a bond might store its
redemption and the final coupon, if any).
Next is the rollback method. Again, it calls the corresponding
method in the Lattice class, which performs the heavy-machinery work
of stepping through the tree (or whatever kind of lattice it
models). It reads the current time from the asset, so it knows on what
nodes it is currently sitting; then, a close interplay begins.
The point is, the lattice can’t simply roll the asset back to the
desired time, since there might be all kind of events occurring:
coupon payments, exercises, you name it. Therefore, it just rolls it
back one short step, modifies the asset values accordingly—which
includes both combining nodes and discounting—and then pauses to
ask the asset if there’s anything that needs to be done; that is, to
call the asset’s adjustValues method.
The adjustment is done in two steps, calling first the
preAdjustValues and then the postAdjustValue method. This is done
so that other assets have a chance to perform their own adjustment
between the two; I’ll show an example of this in a later post. Each of
the two methods performs a bit of housekeeping (namely, they store the
time of the latest adjustment so that the asset is not adjusted twice
at the same time; this might happen when composing assets, and would
obviously wreak havoc on the results) and then calls a virtual method
(preAdjustValuesImpl or postAdjustValueImpl, respectively) which
makes the instrument-specific adjustments.
When this is done, the ball is back in the lattice’s field. The lattice rolls back another short step, and the whole thing repeats again and again until the assets reaches the required time.
Finally, the presentValue method returns, well, the present value of
the asset. It is meant to be called by client code after rolling the
asset back to the earliest interesting time—that is, to the time
for which further rolling back to today’s date only involves
discounting and not adjustments of any kind: e.g., it might be the
earliest exercise time of an option or the first coupon time of a
bond. As usual, the asset delegates the calculation by passing itself
to the lattice’s presentValue method; a given lattice implementation
might simply roll the asset back to the present time (if it isn’t
already there, of course) and read its value from the root node,
whereas another lattice might be able to take a shortcut and calculate
the present value as a function of the values on the nodes at the
current time.
As usual, there’s room for improvement. Some of the steps are left as
an implicit requirement; for instance, the fact that the lattice’s
initialize method should call the asset’s reset method, or that
reset must resize the array stored in the asset (in hindsight, the
array should be resized in the lattice’s initialize method before
calling reset. This would minimize repetition, since we’ll write
many more assets than lattices.) However, this is what we have at this
time. In next post, we’ll move on and build some assets.