Pricing over a range of days
Hello again.
In this post, another old notebook originally included in the QuantLib Python Cookbook and updated for publication here. If you are starting to see a pattern, be patient and wait for next month (he said, smiling obscurely).
Pricing over a range of days
Based on questions on Stack Exchange from Charles, bob.jonst, MCM and lcheng.
import QuantLib as ql
import pandas as pd
from matplotlib import pyplot as plt
Let’s say we have an instrument (a fixed-rate bond, for instance) that we want to price on a number of dates. I assume we also have the market quotes, or the curves, corresponding to each of the dates; in this case we only need interest rate information, but the library works the same way for any quotes.
We’ll store the resulting prices in a dictionary, with the date as the key.
prices = {}
Producing a single price
To price the bond on a single date, we set the evaluation date…
today = ql.Date(3, ql.May, 2021)
ql.Settings.instance().evaluationDate = today
…and we create the instrument itself…
start_date = ql.Date(8, ql.February, 2019)
maturity_date = start_date + ql.Period(5, ql.Years)
schedule = ql.Schedule(
start_date,
maturity_date,
ql.Period(ql.Semiannual),
ql.TARGET(),
ql.Following,
ql.Following,
ql.DateGeneration.Backward,
False,
)
coupons = [0.01]
bond = ql.FixedRateBond(
3, 100, schedule, coupons, ql.Thirty360(ql.Thirty360.BondBasis)
)
…and the required discount curve. Here, I’m interpolating it over a set of tabulated rates, such as those I might have available from an external curve service.
data = [
(ql.Period(0, ql.Months), 0.04),
(ql.Period(6, ql.Months), 0.04),
(ql.Period(1, ql.Years), 0.06),
(ql.Period(2, ql.Years), 0.16),
(ql.Period(3, ql.Years), 0.33),
(ql.Period(5, ql.Years), 0.84),
(ql.Period(7, ql.Years), 1.29),
(ql.Period(10, ql.Years), 1.63),
(ql.Period(20, ql.Years), 2.18),
(ql.Period(30, ql.Years), 2.30),
]
dates = [today + p for p, _ in data]
rates = [r / 100 for _, r in data]
discount_curve = ql.ZeroCurve(dates, rates, ql.Actual365Fixed())
Given the bond and the curve, we link them together through an engine and get the result.
discount_handle = ql.RelinkableYieldTermStructureHandle(discount_curve)
bond.setPricingEngine(ql.DiscountingBondEngine(discount_handle))
prices[today] = bond.cleanPrice()
print(prices[today])
101.94609091386468
Pricing on multiple days
Now, let’s say for instance that we have rates for each day from January to April and we want to get the corresponding prices. For this notebook, they’re stored in a file so I don’t need to show you pages of numbers in order to define them. In the real world, they will probably be stored in a DB or some other resource.
df = pd.read_csv(
"./data/multiple-yields.txt", delimiter="\t", parse_dates=["Date"]
)
df
| Date | 0M | 6M | 1Y | … | 10Y | 20Y | 30Y |
|---|---|---|---|---|---|---|---|
| 2021-01-04 | 0.09 | 0.09 | 0.10 | … | 0.93 | 1.46 | 1.66 |
| 2021-01-05 | 0.09 | 0.09 | 0.10 | … | 0.96 | 1.49 | 1.70 |
| 2021-01-06 | 0.09 | 0.09 | 0.11 | … | 1.04 | 1.60 | 1.81 |
| 2021-01-07 | 0.09 | 0.09 | 0.11 | … | 1.08 | 1.64 | 1.85 |
| 2021-01-08 | 0.09 | 0.09 | 0.10 | … | 1.13 | 1.67 | 1.87 |
| … | … | … | … | … | … | … | … |
| 2021-04-26 | 0.04 | 0.04 | 0.06 | … | 1.58 | 2.13 | 2.24 |
| 2021-04-27 | 0.04 | 0.04 | 0.06 | … | 1.63 | 2.18 | 2.29 |
| 2021-04-28 | 0.04 | 0.04 | 0.05 | … | 1.63 | 2.19 | 2.29 |
| 2021-04-29 | 0.04 | 0.04 | 0.05 | … | 1.65 | 2.20 | 2.31 |
| 2021-04-30 | 0.03 | 0.03 | 0.05 | … | 1.65 | 2.19 | 2.30 |
We could repeat the whole calculation for all dates, but it goes against the grain of the library. The architecture (see chapter 2 of Implementing QuantLib for details) was designed so that the instrument can react to changing market conditions; therefore, we can at least avoid recreating the instrument. We’ll still have change the discount curve and the evaluation date.
For instance, here I’ll calculate the price for the first row of data. As I mentioned, I need to set the new evaluation date:
d = ql.Date.from_date(df["Date"][0])
ql.Settings.instance().evaluationDate = d
Then I’ll pick the corresponding rates and rebuild a discount curve:
tenors = list(df.columns[1:])
dates = []
rates = []
for tenor in tenors:
dates.append(ql.Settings.instance().evaluationDate + ql.Period(tenor))
rates.append(df[tenor][0] / 100)
discount_curve = ql.ZeroCurve(dates, rates, ql.Actual365Fixed())
Now I can link the handle in the engine to the new discount curve…
discount_handle.linkTo(discount_curve)
…after which the bond returns the updated price.
print(bond.cleanPrice())
102.55592512367953
By repeating the process, I can generate prices for the whole data set.
for _, row in df.iterrows():
d = ql.Date.from_date(row["Date"])
ql.Settings.instance().evaluationDate = d
dates = []
rates = []
for tenor in tenors:
dates.append(d + ql.Period(tenor))
rates.append(row[tenor] / 100)
discount_curve = ql.ZeroCurve(dates, rates, ql.Actual365Fixed())
discount_handle.linkTo(discount_curve)
prices[d] = bond.cleanPrice()
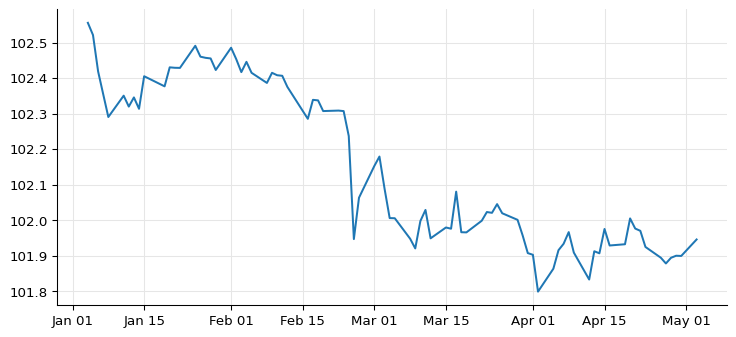
Here are the results.
dates, values = zip(*sorted(prices.items()))
ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.plot([d.to_date() for d in dates], values, "-");
Using quotes
If we work with quotes, we can also avoid rebuilding the curve. Let’s say our discount curve is defined as a risk-free curve with an additional credit spread. The risk-free curve is bootstrapped from a number of market rates; for simplicity, here I’ll use a set of overnight interest-rate swaps, but you’ll use whatever makes sense in your case.
index = ql.Estr()
tenors = [ql.Period(i, ql.Years) for i in range(1, 11)]
rates = [
0.010,
0.012,
0.013,
0.014,
0.016,
0.017,
0.018,
0.020,
0.021,
0.022,
]
quotes = []
helpers = []
for tenor, rate in zip(tenors, rates):
q = ql.SimpleQuote(rate)
h = ql.OISRateHelper(2, tenor, ql.QuoteHandle(q), index)
quotes.append(q)
helpers.append(h)
One thing to note: I’ll setup the curve so that it moves with the evaluation date. This means that I won’t pass an explicit reference date, but a number of business days and a calendar. Passing 0, as in this case, will cause the reference date of the curve to always equal the evaluation date, whatever it happens to be at any given moment; while passing 2, for instance, would cause it to equal the corresponding spot date.
risk_free_curve = ql.PiecewiseFlatForward(
0, ql.TARGET(), helpers, ql.Actual360()
)
Finally, I’ll manage credit as an additional spread over the curve:
spread = ql.SimpleQuote(0.01)
discount_curve = ql.ZeroSpreadedTermStructure(
ql.YieldTermStructureHandle(risk_free_curve), ql.QuoteHandle(spread)
)
Now we can recalculate today’s price:
ql.Settings.instance().evaluationDate = today
discount_handle.linkTo(discount_curve)
prices[today] = bond.cleanPrice()
print(prices[today])
96.48182194290018
Multiple days again
As before, I’ll now assume to have quotes stored for the past four months; and again, I’ll read the quotes from a file.
df = pd.read_csv(
"./data/multiple-quotes.txt", delimiter="\t", parse_dates=["date"]
)
df
| date | 1Y | 2Y | 3Y | … | 9Y | 10Y | spread |
|---|---|---|---|---|---|---|---|
| 2021-01-04 | 0.60 | 0.77 | 0.90 | … | 1.70 | 1.76 | 0.31 |
| 2021-01-05 | 0.59 | 0.77 | 0.91 | … | 1.72 | 1.77 | 0.35 |
| 2021-01-06 | 0.59 | 0.80 | 0.87 | … | 1.77 | 1.74 | 0.33 |
| 2021-01-07 | 0.58 | 0.81 | 0.88 | … | 1.77 | 1.74 | 0.40 |
| 2021-01-08 | 0.60 | 0.77 | 0.92 | … | 1.68 | 1.80 | 0.36 |
| … | … | … | … | … | … | … | … |
| 2021-04-26 | 0.94 | 1.20 | 1.32 | … | 2.16 | 2.21 | 1.12 |
| 2021-04-27 | 0.96 | 1.15 | 1.29 | … | 2.11 | 2.19 | 0.99 |
| 2021-04-28 | 0.98 | 1.18 | 1.30 | … | 2.11 | 2.24 | 1.08 |
| 2021-04-29 | 0.96 | 1.20 | 1.28 | … | 2.14 | 2.29 | 0.97 |
| 2021-04-30 | 1.00 | 1.17 | 1.30 | … | 2.13 | 2.16 | 1.01 |
Now that we created the curve based on quotes, we don’t need to build a new one at each step. Instead, we can set new values to the quotes and they will trigger the necessary recalculations in the curve and the instrument.
prices = {}
for _, row in df.iterrows():
date = ql.Date.from_date(row["date"])
for q, tenor in zip(
quotes,
["1Y", "2Y", "3Y", "4Y", "5Y", "6Y", "7Y", "8Y", "9Y", "10Y"],
):
q.setValue(row[tenor] / 100)
spread.setValue(row["spread"] / 100)
ql.Settings.instance().evaluationDate = date
prices[date] = bond.cleanPrice()
Note that we didn’t create any new object in the loop; we’re only settings new values to the quotes.
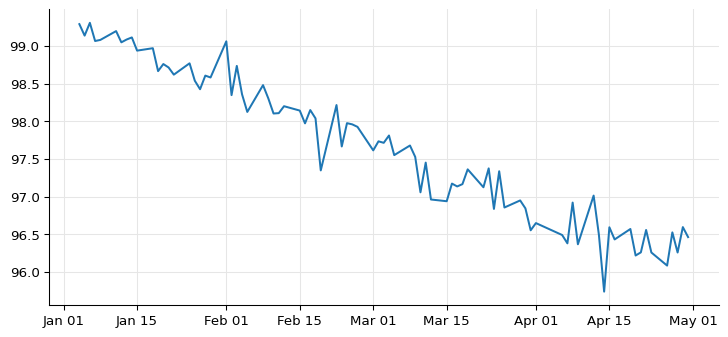
Again, here are the results:
dates, values = zip(*sorted(prices.items()))
ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.plot([d.to_date() for d in dates], values, "-");
A complication: past fixings
For instruments that depend on the floating rate, we might need some past fixings. This is not necessarily related to pricing on a range of dates: even on today’s date, we need the fixing for the current coupon. Let’s set the instrument up…
forecast_handle = ql.YieldTermStructureHandle(risk_free_curve)
index = ql.Euribor6M(forecast_handle)
bond = ql.FloatingRateBond(
3, 100, schedule, index, ql.Thirty360(ql.Thirty360.BondBasis)
)
bond.setPricingEngine(ql.DiscountingBondEngine(discount_handle))
ql.Settings.instance().evaluationDate = today
for q, r in zip(quotes, rates):
q.setValue(r)
spread.setValue(0.01)
…and try to price it. No joy.
try:
print(bond.cleanPrice())
except Exception as e:
print(f"{type(e).__name__}: {e}")
RuntimeError: Missing Euribor6M Actual/360 fixing for February 4th, 2021
Being in the past, the fixing can’t be retrieved from the curve. We have to store it into the index, after which the calculation works:
index.addFixing(ql.Date(4, ql.February, 2021), 0.005)
print(bond.cleanPrice())
97.09258058529258
When pricing on a range of dates, though, we need to take into account the fact that the current coupon changes as we go back in time. These two dates will work…
ql.Settings.instance().evaluationDate = ql.Date(1, ql.March, 2021)
print(bond.cleanPrice())
ql.Settings.instance().evaluationDate = ql.Date(15, ql.February, 2021)
print(bond.cleanPrice())
96.84054989393012
96.78778930005275
…but this one causes the previous coupon to be evaluated, and that requires a new fixing:
ql.Settings.instance().evaluationDate = ql.Date(1, ql.February, 2021)
try:
print(bond.cleanPrice())
except Exception as e:
print(f"{type(e).__name__}: {e}")
RuntimeError: Missing Euribor6M Actual/360 fixing for August 6th, 2020
Once we add it, the calculation works again.
index.addFixing(ql.Date(6, ql.August, 2020), 0.004)
print(bond.cleanPrice())
96.97859587521839
(If you’re wondering how the calculation worked before, since this coupon belonged to the bond: on the other evaluation dates, this coupon was expired and the engine could skip it without needing to calculate its amount. Thus, its fixing didn’t need to be retrieved.)
More complications: future past fixings
What if we go forward in time, instead of pricing on past dates?
For one thing, we’ll need to forecast curves in some way. One way is to imply them from today’s curves: I talk about implied curves in another notebook, so I won’t repeat myself here. Let’s assume we have implied rates and we can set them. Once we do, we can price in the future just as easily as we do in the past.
ql.Settings.instance().evaluationDate = ql.Date(1, ql.June, 2021)
print(bond.cleanPrice())
97.2097212826188
However, there’s another problem, as pointed out by Mariano Zeron in a post to the QuantLib mailing list. If we go further in the future, the bond will require—so to speak—future past fixings.
ql.Settings.instance().evaluationDate = ql.Date(1, ql.September, 2021)
try:
print(bond.cleanPrice())
except Exception as e:
print(f"{type(e).__name__}: {e}")
RuntimeError: Missing Euribor6M Actual/360 fixing for August 5th, 2021
Here the curve starts on September 1st 2021, and cannot retrieve the fixing at the start of the corresponding coupon.
One way out of this might be to forecast fixings off the current curve and store them:
ql.Settings.instance().evaluationDate = today
fixing_date = ql.Date(5, ql.August, 2021)
future_fixing = index.fixing(fixing_date)
print(future_fixing)
index.addFixing(fixing_date, future_fixing)
0.009974987403789588
This way, they will be retrieved in the same way as real past fixings.
ql.Settings.instance().evaluationDate = ql.Date(1, ql.September, 2021)
print(bond.cleanPrice())
97.55258650460641
Of course, you might forecast them in a better way: that’s up to you. And if you’re worried that this might interfere with pricing on today’s date, don’t: stored fixings are only used if they’re in the past with respect to the evaluation date. The fixing I’m storing below for February 3rd 2022 will be retrieved if the evaluation date is later…
index.addFixing(ql.Date(3, ql.February, 2022), 0.02)
ql.Settings.instance().evaluationDate = ql.Date(1, ql.June, 2022)
print(index.fixing(ql.Date(3, ql.February, 2022)))
0.02
…but it will be forecast from the curve when it’s after the evaluation date:
ql.Settings.instance().evaluationDate = today
print(index.fixing(ql.Date(3, ql.February, 2022)))
0.012063742194402307