Updating multiple market quotes

Hello, dear reader.

Like a householder who brings out of his treasure what is new and what is old, this time I’m posting an updated version of a notebook whose old version is included in the QuantLib Python Cookbook. I hope you find it useful. Here we go.

We have already seen in other examples how instances of SimpleQuote can be updated and how they notify their observers. In this notebook, I’ll show a possible pitfall to avoid when multiple quotes need to be updated.

import numpy as np
from matplotlib import pyplot as plt
import QuantLib as ql

today = ql.Date(17, ql.October, 2016)
ql.Settings.instance().evaluationDate = today

Setting the stage

For illustration purposes, I’ll create a bond curve using the same data and algorithm shown in one of the QuantLib C++ examples; namely, I’ll give to the curve the functional form defined by the Nelson-Siegel model and I’ll fit it to a number of bonds. Here are the maturities in years and the coupons of the bonds I’ll use:

data = [
    (2, 0.02),
    (4, 0.0225),
    (6, 0.025),
    (8, 0.0275),
    (10, 0.03),
    (12, 0.0325),
    (14, 0.035),
    (16, 0.0375),
    (18, 0.04),
    (20, 0.0425),
    (22, 0.045),
    (24, 0.0475),
    (26, 0.05),
    (28, 0.0525),
    (30, 0.055),
]

For simplicity, I’ll use the same start date, frequency and conventions for all the bonds; this doesn’t affect the point I’m going to make in the rest of the notebook. I’ll also assume that all bonds currently price at 100. Of course, this is not a requirement for the fit: when using real data, each bond will have its own schedule and price.

I’ll skip over the details of building the curve now; the one thing you’ll need to remember is that it depends on the input quotes modeling the bond prices.

calendar = ql.TARGET()
settlement = calendar.advance(today, 3, ql.Days)
quotes = []
helpers = []
for length, coupon in data:
    maturity = calendar.advance(settlement, length, ql.Years)
    schedule = ql.Schedule(
        settlement,
        maturity,
        ql.Period(ql.Annual),
        calendar,
        ql.ModifiedFollowing,
        ql.ModifiedFollowing,
        ql.DateGeneration.Backward,
        False,
    )
    quote = ql.SimpleQuote(100.0)
    quotes.append(quote)
    helpers.append(
        ql.FixedRateBondHelper(
            ql.QuoteHandle(quote),
            3,
            100.0,
            schedule,
            [coupon],
            ql.SimpleDayCounter(),
            ql.ModifiedFollowing,
        )
    )

curve = ql.FittedBondDiscountCurve(
    0, calendar, helpers, ql.SimpleDayCounter(), ql.NelsonSiegelFitting()
)

Just for kicks, here is a visualization of the curve as discount factors versus time in years:

sample_times = np.linspace(0.0, 30.0, 301)
sample_discounts = [curve.discount(t) for t in sample_times]

ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
ax.set_ylim(0.0, 1.0)
ax.plot(sample_times, sample_discounts);

And here is a bond priced by discounting its coupons on the curve:

schedule = ql.Schedule(
    today,
    calendar.advance(today, 15, ql.Years),
    ql.Period(ql.Semiannual),
    calendar,
    ql.ModifiedFollowing,
    ql.ModifiedFollowing,
    ql.DateGeneration.Backward,
    False,
)
bond = ql.FixedRateBond(3, 100.0, schedule, [0.04], ql.Actual360())
bond.setPricingEngine(
    ql.DiscountingBondEngine(ql.YieldTermStructureHandle(curve))
)
print(bond.cleanPrice())

105.77449627458306

“It looked like a good idea at the time”

The bond we created is, indirectly, an observer of the market quotes. However, it is also an observable, and will forward to its own observers (if any) the notifications it receives.

Therefore, if you’re writing some kind of interactive application, it might be tempting to add an observer that checks whether the bond is out of date, and (if so) recalculates the bond and outputs its new price. In Python, I can do this by creating an instance of Observer (with a function to be executed when it receives a notification) and by registering it with the bond.

As a reminder of how the whole thing works: the changes will come from the market quotes, but the observer doesn’t need to be concerned with that and only registers with the object it’s ultimately interested in; in this case, the bond whose price it wants to monitor. A change in any of the market quotes will cause the quote to notify the corresponding helper, which in turn will notify the curve, and so on; the notification will reach the pricing engine, the bond and finally our observer.

prices = []


def print_price():
    p = bond.cleanPrice()
    prices.append(p)
    print(p)


o = ql.Observer(print_price)
o.registerWith(bond)

The function we created also appends the new price to a list, that can be used later as a history of the prices. Let’s see if it works: when we set a new value to one of the quotes, print_price should be called and a bond price should be printed out.

quotes[2].setValue(101.0)

105.77449627458306
105.86560416829894

Whoa, what was that? The function was called twice, which surprised me too when I wrote this notebook. It turns out that, due to a glitch of multiple inheritance, the curve sends two notifications to the instrument. After the first, the instrument recalculates but the curve doesn’t (which explains why the price doesn’t change); after the second, the curve updates and the price changes. This should be fixed in a future release.

Let’s set the quote back to its original value.

quotes[2].setValue(100.0)

105.86560416829894
105.77449623091606

Now, let’s say the market moves up and, accordingly, all the bonds prices increase to 101. Therefore, we need to update all the quotes.

prices = []
for q in quotes:
    q.setValue(101.0)

77449623091606
2838840874108
2838840874108
21862925930098
21862925930098
31959069144436
31959069144436
48786663523776
48786663523776
68032070019959
68032070019959
87580390525216
87580390525216
06201692440669
06201692440669
23044635889315
23044635889315
37409242335241
37409242335241
48708841640764
48708841640764
56505211620107
56505211620107
60570737717579
60570737717579
60980192172282
60980192172282
58011151613943
58011151613943
52070702691613

As you see, each of the updates sent a notification and thus triggered a recalculation. We can use the list of prices we collected (slicing it to skip duplicate values) to visualize how the price changed.

initial_price = prices[0]
updated_prices = prices[1::2]
ax = plt.figure(figsize=(9, 4)).add_subplot(1, 1, 1)
p, = ax.plot([initial_price] + updated_prices, "-")
ax.plot(0, initial_price, 'o', color=p.get_color())
ax.plot(len(updated_prices), updated_prices[-1], 'o', color=p.get_color());

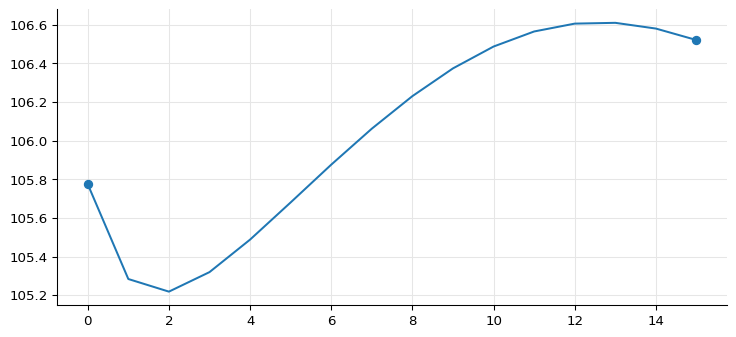
The first value is the original bond price, and the last value is the final price after all the quotes were updated; but all the prices in between were calculated based on an incomplete set of changes in which some quotes were updated and some others weren’t. They are all incorrect, and (since they went both above and below the range of the real prices) also outright dangerous: in case your application defined any triggers on price levels, they might have fired incorrectly. Clearly, this is not the kind of behavior we want our code to have.

Alternatives?

There are workarounds we can apply. For instance, it’s possible to freeze the bond temporarily, preventing it from forwarding notifications.

bond.freeze()

Now, notifications won’t be forwarded by the bond and thus won’t reach our observer. In fact, the following loop won’t print anything.

for q in quotes:
    q.setValue(101.5)

When we restore the bond, it sends a single notification, which triggers only one recalculation and gives the correct final price.

bond.unfreeze()

106.85839342065753

When using C++, it’s also possible to disable and re-enable notifications globally, which makes it more convenient.

But it all feels a bit convoluted anyway, and if you have to keep track of your bonds and call freeze and unfreeze you might as well ask them for their new price instead. The whole thing will be simpler if we discard the initial idea and don’t force a recalculation for each notification.

Pull, don’t push

It’s preferable for updates to not trigger recalculation, just like the instruments in the library do. This way, you can control when the calculation occur.

To do so, let’s remove the observer we have in place.

del o

Our application code knows when a set of changes is published together (reflecting a change of the whole market subset we’re tracking). Therefore, it should apply all the changes, and only afterwards it should send some kind of application-level notification that your bonds should be asked for new prices. The ones that depend on the changed quotes will have received their notifications, and will recalculate when asked for a price; other bonds that don’t depend on the changed quotes won’t have received any notifications and won’t recalculate.

for q in quotes:
    q.setValue(101.0)

bond.cleanPrice()

106.52070699239374