Adding a new cash flow to QuantLib, part I
Welcome back.
Today’s post was originally published in the July 2024 issue of Wilmott Magazine. The full source code is available on my Tutorial page, together with code from other articles and, when available, either the articles themselves or corresponding blog posts like this one.
Subscribe to my Substack to receive my posts in your inbox, or follow me on Twitter or LinkedIn if you want to be notified of new posts, or subscribe via RSS if you’re the tech type: the buttons for all that are in the footer. Also, I’m available for training, both online and (when possible) on-site: visit my Training page for more information.
Adding a new cash flow to QuantLib, part I
Welcome back. In the May 2024 issue, we looked at generating bond cash flows with a given schedule. It was from the point of view of using the existing features of the library.
This post changes focus and discusses the internal design of the library with the purpose to extend it. Is QuantLib’s reputation for over-engineering well deserved? You’ll be the judge, dear reader.
A new kind of coupon
As I write this, in late March 2024, some QuantLib contributors are discussing one particular kind of coupon which is not currently implemented: a short stub at the beginning of a floating-rate bond (or an interest-rate swap) whose rate must be interpolated between the fixings of two quoted indexes. Just to make an example, it might be a four-months coupon whose rate should be interpolated between the quoted three-months and six-months Euribor fixings.
By the time you read this, the library might have an implementation available. On this side of the publication lag, though, that didn’t happen yet; which made me think of writing this article as a way to clear my own ideas. First, I’ll describe the existing structure in which it should be inserted. In the next article, I’ll list a few possible ways to do it and comment on the pros and cons of each.
Will we find a sensible implementation? Will the current design bite us back? Since Wilmott Magazine doesn’t provide audio features, I’ll leave it to you to insert an appropriately suspenseful chord here.
The status quo
The implementation of cash flows is the subject of a full chapter in my Implementing QuantLib book, and you can find drafts of it in my blog if you don’t feel like heading to Amazon. Here are the Cliff’s notes.
There is a whole hierarchy of cash flows in the library, and you can see a sketch of part of it in the following figure.
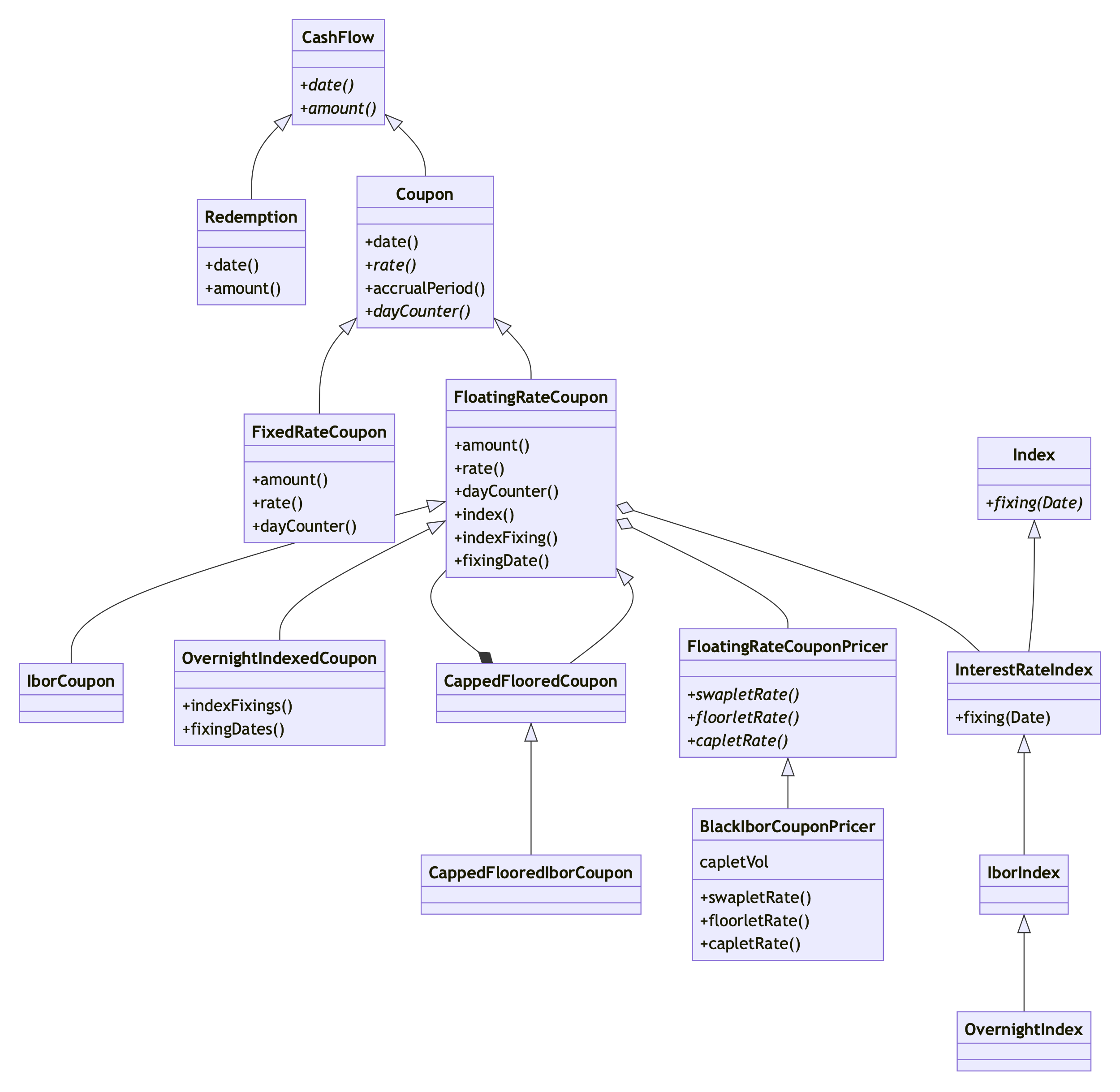
The parent class, CashFlow, has only a minimal interface; it can
return the date and the amount of the payment—I’m glossing over a
few other methods, coming from the fact that CashFlow in turn
inherits from other classes (for instance, the LazyObject class I
described in the November 2023 issue in the context of the Observer
pattern) and that it participates in the Acyclic Visitor pattern, too.
Simple cash flows
For some cash flows, date and amount are all there is; that’s the case
for the Redemption class, modeling the final payment of a bond. The
same goes for any amortizing payments during the life of a bond.
More interesting cash flows
A number of other cash flows can be implemented under the umbrella of
the Coupon base class, modeling any payment that comes from accruing
an interest rate over a period. Yes, that was a dad joke in the
heading above. Force of habit.
The Coupon class adds several other methods to the interface of
CashFlow. Some of them return information on the rate, the nominal
upon which the interest is paid, the start and end date of the coupon,
the day-count convention used to calculate the corresponding accrual
time, and any ex-coupon period if that’s the case; and others return
calculated results such as the accrued amount at any given date. They
are a mixture of virtual and non-virtual methods; there is some method
in the madness, but I’m not going into it in this article. Cliff’s
notes, as I said.
The simplest class that derives from Coupon is probably
FixedRateCoupon. The interest rate is a given, so there’s no
particular calculation to do in order to return the total coupon
amount or the accrued amount at a given date. However, the
implementation is not as simple as I would like (a common theme in the
library, unfortunately) in order to allow some more outlandish coupons
in which the rate is specified as a compounded or continuous rate.
The sorrows of floating-rate coupons
In Implementing QuantLib, I wrote: “The FloatingRateCoupon class
is emblematic of the life of most software. It started simple, became
more complex as time went by, and might now need some refactoring; its
current implementation has a number of issues that I’ll point out as I
describe it.”
As you can see, I would have made a very poor salesman.
This class models coupons that pay an interest rate based on the fixing of some index. The most common case used to be some kind of LIBOR-like index, but it could also be, for instance, a quoted swap rate in the case of the floating coupons of a constant-maturity swap. You’re surely thinking of another example right now, aren’t you?
To generalize over all of these cases, its constructor takes an
instance (ok, a pointer to an instance) of the abstract
InterestRateIndex base class, from which actual indexes are
inherited; the index is responsible for providing its fixings, either
by forecasting future ones or by storing past ones.
The FloatingRateCoupon class adds a number of methods to the
interface of Coupon; you can see some of them in the figure above,
but they’re by no means the only ones. The interested reader—that
mythical figure—can find them in the library code or in
Implementing QuantLib. Derived classes such as IborCoupon (a
coupon that pays the fixing of an index such as Euribor, or LIBOR
until the recent past) implement them using the relevant conventions,
and their constructors restrict the kind of interest-rate index they
can accept.
Now, FloatingRateCoupon looks harmless at first, but it already has
some assumptions baked in; some of those might bite back, and a few
have already done so. For instance, it has a fixingDate method and
an indexFixing method; their signature assumes that the coupon rate
is fixed at one single date, based on a single index fixing. As you
can imagine, this hasn’t aged well now that coupons based on average
SOFR fixings are the new normal. In fact, as shown in the diagram,
the OvernightIndexedCoupon class (which models such coupons) had to
ignore the inherited interface and declare a new, sensible one for its
use case.
And of course, the other big assumption is that the coupon is based on the fixing of one single index. It doesn’t look good when you remember that we need to interpolate between two of them, does it?
An example: a floating-rate bond
I don’t want to be a downer, though. These coupon work, after all: in
the following code, you can see an example where most of the complexity is
hidden behind the scenes: we can instantiate a simple floating-rate
bond by building its coupon schedule, creating an instance of the
index to be paid, and passing everything to the constructor of the
FloatingRateBond class.
auto today = Date(18, March, 2024);
Settings::instance().evaluationDate() = today;
IborCoupon::Settings::instance().createIndexedCoupons();
auto forecastCurve = ext::make_shared<FlatForward>(
today, 0.04, Actual360());
auto index6m = ext::make_shared<Euribor6M>(
Handle<YieldTermStructure>(forecastCurve));
index6m->addFixing(Date(6, February, 2023), 0.03008);
index6m->addFixing(Date(4, August, 2023), 0.0394);
index6m->addFixing(Date(6, February, 2024), 0.03922);
Schedule schedule =
MakeSchedule()
.from(Date(8, February, 2023))
.to(Date(8, February, 2028))
.withFrequency(Semiannual)
.withCalendar(TARGET())
.backwards();
int settlementDays = 3;
double faceAmount = 1000000.0;
auto dayCounter = index6m->dayCounter();
FloatingRateBond bond(settlementDays, faceAmount,
schedule, index6m,
dayCounter);
The index needs a forecast curve to return estimates of future fixings, and needs to store the past fixings we need (or, if you’re not writing a self-contained example, their whole history loaded from a DB.) Once everything is set up, the resulting bond can give you the cash flows shown in the following table, and can be priced given a discount curve or a yield (not shown here).
| date | nominal | fixing | rate | amount |
|---|---|---|---|---|
| 2023-08-08 | 1000000.00 | 3.008 | 3.008 | 15123.56 |
| 2024-02-08 | 1000000.00 | 3.940 | 3.940 | 20137.78 |
| 2024-08-08 | 1000000.00 | 3.922 | 3.922 | 19827.89 |
| 2025-02-10 | 1000000.00 | 4.042 | 4.042 | 20881.70 |
| 2025-08-08 | 1000000.00 | 4.041 | 4.041 | 20091.35 |
| 2026-02-09 | 1000000.00 | 4.041 | 4.041 | 20768.28 |
| 2026-08-10 | 1000000.00 | 4.041 | 4.041 | 20428.08 |
| 2027-02-08 | 1000000.00 | 4.041 | 4.041 | 20430.35 |
| 2027-08-09 | 1000000.00 | 4.041 | 4.041 | 20428.08 |
| 2028-02-08 | 1000000.00 | 4.041 | 4.041 | 20542.61 |
| 2028-02-08 | n/a | n/a | n/a | 1000000.00 |
Adding a floor
Unfortunately, sometimes we have to get a bit more under the hood. For instance, if we want our coupons to have a floor, we need (as shown in the next bit of code) first to create them and then to give them a pricer. The latter knows how to deal with the optionality and contains the required additional market data, such as the volatility of the rate in this case.
Leg coupons =
IborLeg(schedule, index6m)
.withNotionals(faceAmount)
.withPaymentDayCounter(dayCounter)
.withFloors(0.01);
auto volatility =
ext::make_shared<ConstantOptionletVolatility>(
today, TARGET(), Following, 0.25,
Actual360(), ShiftedLognormal, 0.01);
auto pricer =
ext::make_shared<BlackIborCouponPricer>(
Handle<OptionletVolatilityStructure>(volatility));
setCouponPricer(coupons, pricer);
Date issueDate = schedule[0];
Bond floored(settlementDays,
schedule.calendar(),
issueDate,
coupons);
The cash flows of the resulting bond are shown in the next table; you can see that the expected rate increases due to the floor and no longer equals the index fixing.
| date | nominal | fixing | rate | amount |
|---|---|---|---|---|
| 2023-08-08 | 1000000.00 | 3.008 | 3.008 | 15123.56 |
| 2024-02-08 | 1000000.00 | 3.940 | 3.940 | 20137.78 |
| 2024-08-08 | 1000000.00 | 3.922 | 3.922 | 19827.89 |
| 2025-02-10 | 1000000.00 | 4.042 | 4.042 | 20881.70 |
| 2025-08-08 | 1000000.00 | 4.041 | 4.041 | 20091.39 |
| 2026-02-09 | 1000000.00 | 4.041 | 4.042 | 20769.47 |
| 2026-08-10 | 1000000.00 | 4.041 | 4.042 | 20434.43 |
| 2027-02-08 | 1000000.00 | 4.041 | 4.045 | 20448.25 |
| 2027-08-09 | 1000000.00 | 4.041 | 4.048 | 20464.74 |
| 2028-02-08 | 1000000.00 | 4.041 | 4.054 | 20605.32 |
| 2028-02-08 | n/a | n/a | n/a | 1000000.00 |
This doesn’t add a lot of code to the example, compared to the simpler case; but supporting this case adds complexity to the cash flow hierarchy. As you can see from the figure above, a separate class deals with capped and/or floored coupons. This makes me itch every time I see it, because it means that a floored LIBOR coupon is not (in the sense of inheritance) a LIBOR coupon.
And of course, we need to introduce a hierarchy of pricers. But I won’t go in any detail about them; again, you know where to look if you’re interested.
Next time: interpolated stub coupons
Now, to go back to our desired new coupon: where should we place it in the cash flow hierarchy? The answer will have to wait for the next installment; and as I mentioned, it’s not entirely clear to me as of now. The seemingly obvious choices might have it inherit the wrong interface, or the wrong constraints. It might turn out to be a study in picking the lesser evil. Such is the interesting life of the library writer.
See you next time!