Chapter 8, part 8 of n: finite-difference meshers
Hello everybody.
I don’t have any news this week. However, there’s always the ongoing series of posts on the new finite-difference framework. And of course, you can catch up to last week’s news if you missed them.
Follow me on Twitter if you want to be notified of new posts, or add me to your Google+ circles, or subscribe via RSS: the buttons for that are in the footer. Also, make sure to check my Training page.
Meshers
The first component to be built is an instance of the Fdm1dMesher
class, shown in the listing that follows; or more precisely, an
instance of its derived FdmBlackScholesMesher class. Each instance
of Fdm1dMesher stores the discretization of one dimension of the
problem domain; in this case we need only one, modeling the desired
range for the underlying value.
class Fdm1dMesher {
public:
Fdm1dMesher(Size size);
Size size() const;
Real dplus(Size index) const;
Real dminus(Size index) const;
Real location(Size index) const;
const std::vector<Real>& locations();
protected:
std::vector<Real> locations_;
std::vector<Real> dplus_, dminus_;
};
The base class doesn’t have behavior, apart from a few inspectors. It
stores a vector named locations_ that contains a set of points \(
{ x_0, x_1, \ldots, x_{n-1} } \) discretizing the domain for \( x
\); and for convenience, it also precomputes two other vectors
dplus_ and dminus_ whose \( i \)-th elements contain \(
(x_{i+1}-x_i) \) and \( (x_i-x_{i-1}) \), respectively. The
vectors are declared as protected, since filling them is left as an
exercise to the constructors of derived classes.
Even if its instances are passed around as shared_ptrs, the class is
not polymorphic; none of the methods in the interface are
virtual. (The class doesn’t even have a virtual destructor, which
might cause undefined behavior in case a pointer to the base class is
deleted as such. In this case, we’re safe thanks to the constructor of
shared_ptr, which stores the correct deleter for the specific
pointer type it was passed.) In fact, there seems to be no reason for
passing instances around as pointers, except maybe to avoid copying;
and even this might not matter (or wouldn’t even hold if you’re
compiling in C++11 mode). In hindsight, the Fdm1dMesher class could
have been written as a class not meant for inheritance, with its
derived classes being replaced by functions building and returning
actual Fdm1dMesher instances.
The FdmBlackScholesMesher constructor, that I won’t show here,
performs a few calculations to determine the grid boundaries based on
the current value of the underlying, its expected variance from now to
the maturity of the option, and possibly some external constraints
(such as barriers, for instance). It is meant to be used not only in
this engine, but also in others for which the underlying follows the
same process. The calculations are similar to those implemented in
the old framework by the FDVanillaEngine class, except that the
new code allows you to tune some of the parameters hard-coded in the
old one; and like in the old framework, the grid is actually for the
logarithm of the underlying.
After calculating the boundaries, the constructor delegates the actual
construction of the grid to one of two generic utility classes, both
inherited from Fdm1dMesher, and then copies their data; if was
a function as mentioned above, it could just return the resulting mesh
instead.
The simplest of the two classes is named Uniform1dMesher, and does
what its name advertises: it creates an equally-spaced grid between
two given boundaries and with the given number of points. The other
class is used when there are one or more points of particular interest
in the grid, such as the option strike, and is named
Concentrating1dMesher. Its constructors build a grid with a given
number of points, but concentrates them around its so-called critical
points. For each of them the constructor takes the value of the point,
another value to tune the density of the points around it, and a
boolean that specifies whether the critical point should actually
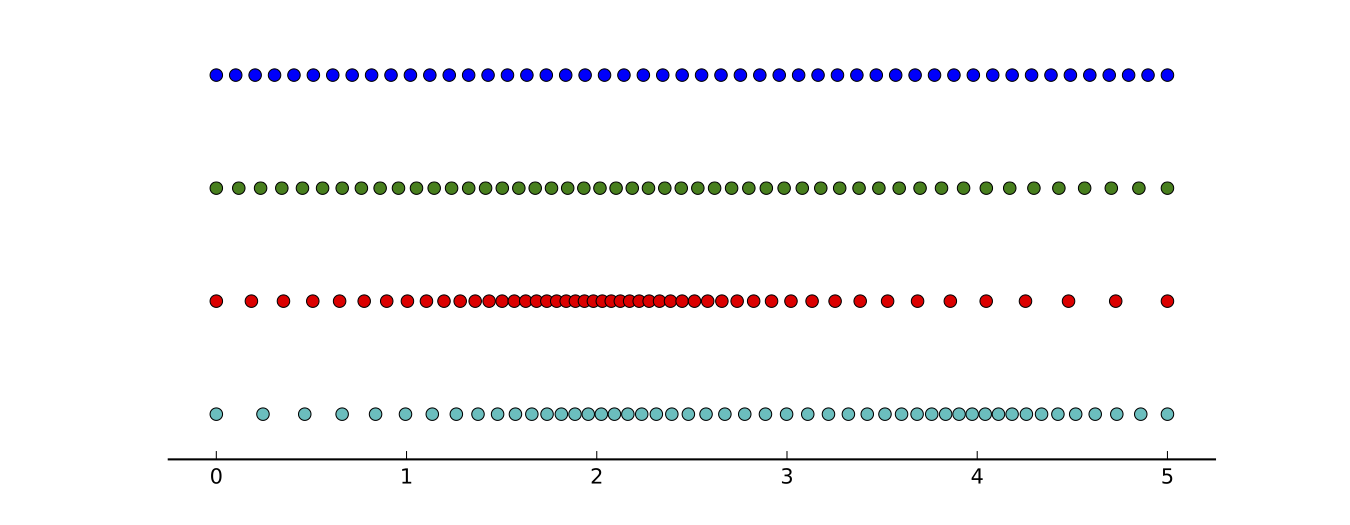
belong to the mesh. The figure below shows some possible resulting
meshes: from top to bottom, a uniform mesh; a concentrating mesh with
a critical point at \( x=2 \); a concentrating mesh with a critical
point at \( x=2 \) and tuned for a higher point density around it;
and a concentrating mesh with critical points at \( x=2 \) and \(
x=4 \). All meshes have the same number of points.
The full multi-dimensional mesh for a finite-difference model is
represented by the abstract FdmMesher class, shown in the next
listing. In the engine shown in the previous post, we’re actually instantiating
the derived FdmMesherComposite class (also shown in the listing),
which builds the full mesh by composing a 1-D mesh for every dimension
of the problem; in this particular case, only the one we built for the
underlying value.
class FdmMesher {
public:
FdmMesher(const shared_ptr<FdmLinearOpLayout>&);
virtual ~FdmMesher() {}
virtual Real dplus(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Real dminus(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Real location(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Array locations(Size direction) const = 0;
const shared_ptr<FdmLinearOpLayout>& layout() const;
};
class FdmMesherComposite : public FdmMesher {
public:
explicit FdmMesherComposite(
const shared_ptr<Fdm1dMesher>& mesher);
FdmMesherComposite(
const shared_ptr<Fdm1dMesher>& m1,
const shared_ptr<Fdm1dMesher>& m2);
// ... constructors for up to 4 meshers ...
explicit FdmMesherComposite(
const std::vector<shared_ptr<Fdm1dMesher> >&);
Real dplus(const FdmLinearOpIterator& iter,
Size direction) const;
Real dminus(const FdmLinearOpIterator& iter,
Size direction) const;
Real location(const FdmLinearOpIterator& iter,
Size direction) const;
Array locations(Size direction) const;
};
Unfortunately, I can’t explain the interface of FdmMesher in full
without going a bit down a rabbit hole. The idea is that, for any
given point in the full mesh (specified through some kind of iterator)
its methods can give the location and the increments dplus and
dminus along any of the dimensions. But to understand it more
clearly, we have first to look at the representation of
multi-dimensional differential operators and arrays; I’ll describe it
in the next post or two.