The strange case of the changing implied term structure
Hello again.
A quick note on the book chapters available in PDF form. Last month, Creative Commons released version 4.0 of their licenses; so from now on, the available material is released under an Attribution-NonCommercial-NoDerivatives 4.0 International license. Your rights (and mine) remain the same under the new license; but, in the words of Creative Commons, it is more user-friendly and more internationally robust.
Onwards to the content of this post. As I mentioned in the past, sometimes questions about QuantLib are asked on the Quantitative Finance Stack Exchange. One such question was asked recently, and I thought I’d share the answer. It was an interesting question, and it’s a curious enough effect that one wouldn’t think of it in advance (I, for one, surely didn’t). Also, this might be the first in a series of QuantLib recipes. No, I’m not planning another book—I have my hands full enough. But I’m going to need something to write in this blog after the book is done, right?
Follow me on Twitter if you want to be notified of new posts, or add me to your circles, or subscribe via RSS: the buttons for that are in the footer. Also, make sure to check my Training page.
The Strange Case of the Changing Implied Term Structure
The idea of Lisa Ann (hi, and thanks for the question!) was to forecast a future interest-rate curve based on today’s rates, and to use it to estimate some kind of forward price for a bond.
The ImpliedTermStructure class does the job: it takes a given curve,
a future date \( D \), and builds a new curve whose reference date
is \( D \) (that is, a curve that returns a discount factor equal to
1 at \( D \)) and that returns the same forward rates as the
original curve between any two dates \( d_1 \) and \( d_2 \) later
than \( D \). Its implementation is simple enough: you can look at
the code for the details, but the gist of it is that, for any date \(
d > D \), it returns a discount factor \( B’(d) \) equal to \(
B(d)/B(D) \), where the \( B \) are the discounts returned by the
original curve. You can see how for \( d = D \), the discount factor
is \( B(D)/B(D) = 1 \); and for any \( d_1 \) and \( d_2 \), \(
B’(d_1)/B’(d_2) = B(d_1)/B(d_2) \), which preserves the forward rate
between \( d_1 \) and \( d_2 \).
Lisa Ann instantiated the original curve and passed it to an
ImpliedTermStructure instance with a reference date six months from
today. The code was somewhat like the following:
RelinkableHandle<YieldTermStructure> currentCurve;
currentCurve.linkTo(depoSwapTermStructure);
Date futureReference = calendar.advance(todaysDate, 6*Months);
shared_ptr<YieldTermStructure> impliedDiscountCurve =
make_shared<ImpliedTermStructure>(currentCurve, futureReference);A look at the discount factors of the two curves showed that they had been built correctly. As the last step in order to price the bond on the implied curve, Lisa Ann set the evaluation date to the future reference; and to her horror (yes, I’m dramatizing. Bear with me a little, will you?) this action changed the shape of the implied curve.
What had happened? The original curve was built so that it moved with the evaluation date, as described in the posts on term structures. Let’s work it out.
Let’s say that the original curve was like the fictional one shown in this figure; the \( x \)-axis is time and the \( y \)-axis shows instantaneous forward rates. From the figure, you can also see that I’m so stuck in my old ways that I’m still using Gnuplot.
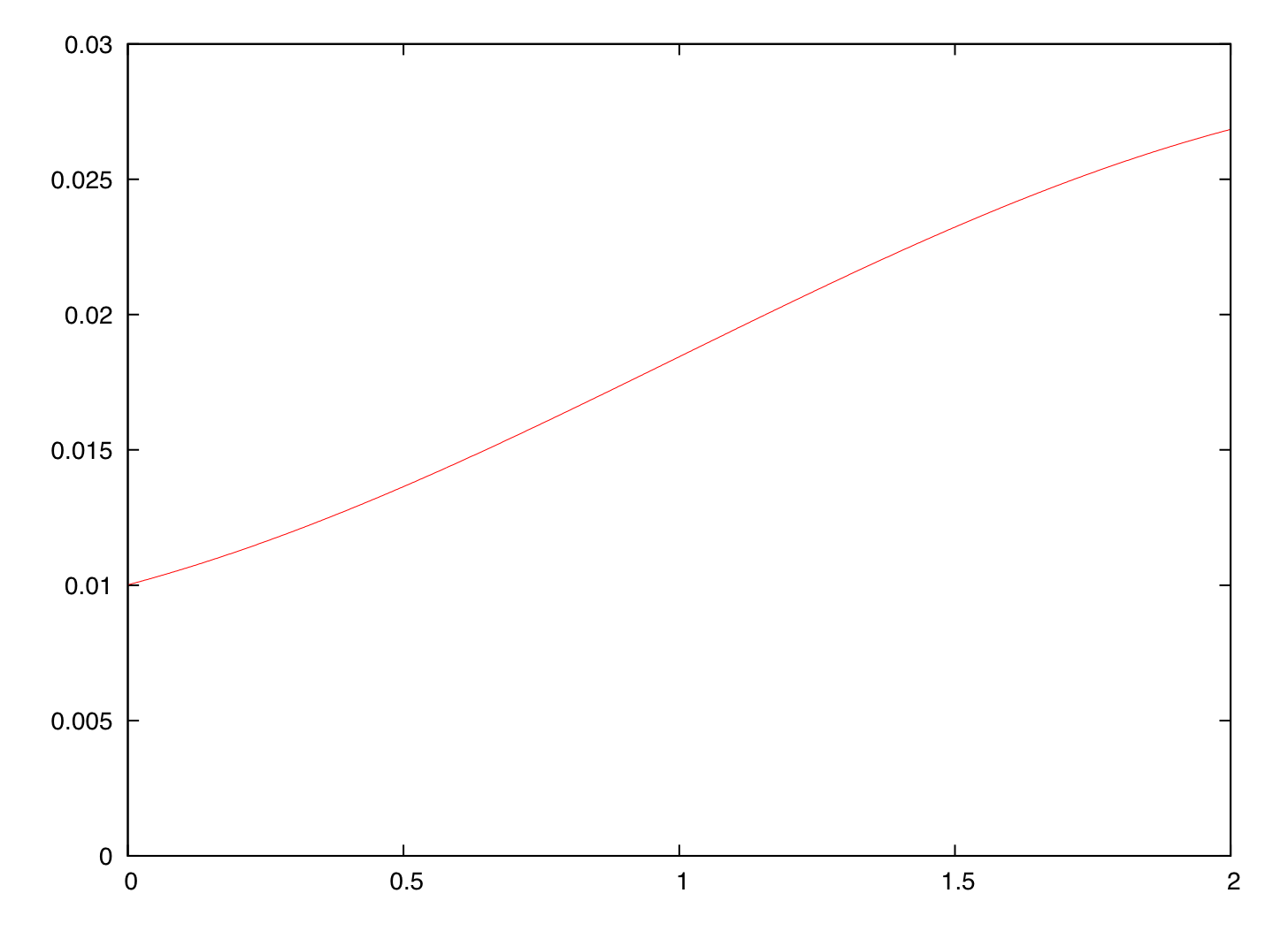
The implied curve had the same rates (so I’m now showing it; it would coincide with the original curve) but started at \( t = 0.5 \).
When the date changed, the original curve was translated verbatim six months in the future, leading to the next figure. The dashed line is the original curve; the solid line is the curve after moving the evaluation date.
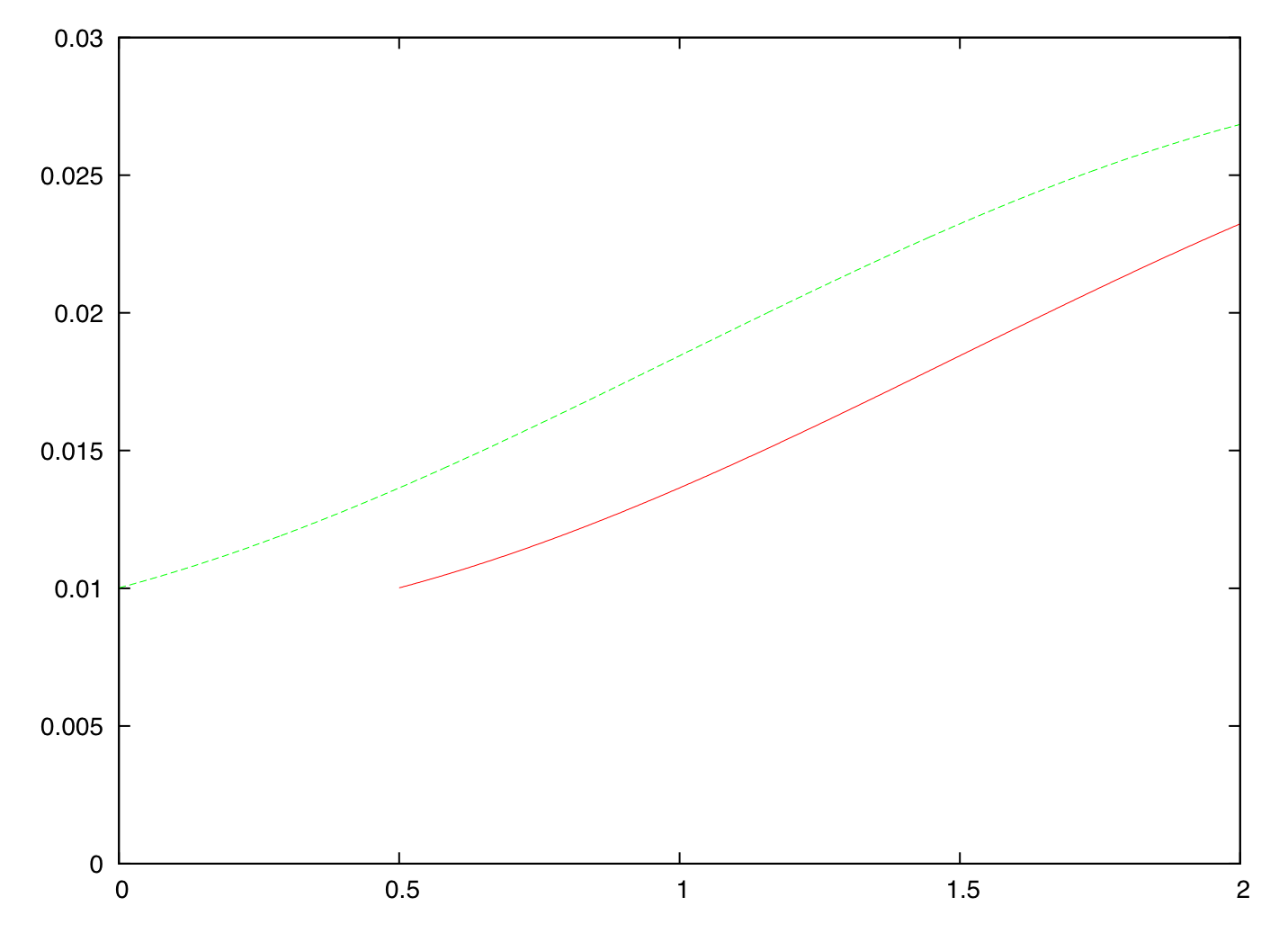
The implied curve was linked to the original one through a handle, and all it could do was to change its rates accordingly.
The solution, as you might have guessed, was to prevent the original curve from moving. In most cases, this can be done by selecting the appropriate constructor; that is, the one that takes an explicit reference date (again, all the details are in this post). This way, the original curve wouldn’t change when the evaluation date moved; and neither would the implied curve.