Chapter 8, part 6 of n: example, American option
Welcome back.
This week, I finally continue with content from chapter 8 (the one on the finite-difference framework, a.k.a. the one that’s taking forever).
Next post will probably be a report from the QuantLib User Meeting, in two or three weeks. There’s probably still places available, so click here for more info.
Follow me on Twitter if you want to be notified of new posts, or add me to your Google+ circles, or subscribe via RSS: the buttons for that are in the footer. Also, make sure to check my Training page.
Example: American option
At this point, writing a finite-difference pricing engine should be just a matter of connecting the dots. Well, not quite. In this section, I’ll sketch the implementation of an American-option engine in QuantLib, which is somewhat more complex than expected (as you can see for yourself from the following figure.)
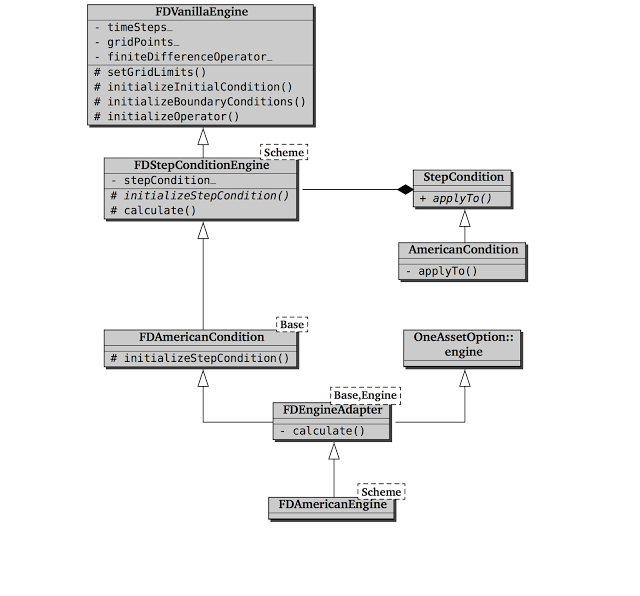
My reasons for doing this are twofold. On the one hand, I nearly got lost myself when I set out to write this chapter and went to read the code of the engine; so I thought it might be useful to put a map out here. On the other hand, this example will help me draw a comparison with the new (and more modular) framework.
Mind you, I’m not dissing the old implementation. The reason it got so complex was that we tried to abstract out reusable chunks of code, which makes perfect sense. The problem is that, although we didn’t see it at the time, inheritance was probably the wrong way to do it.
Let’s start with the FDVanillaEngine class, shown in the listing
below. It can be used as a base class for both vanilla-option and
dividend vanilla-option engines, which might explain why the name is
not as specific as, say, FDVanillaOptionEngine. (We might just have
decided to shorten the name, though. I don’t think anybody remembers
after all these years.)
class FDVanillaEngine {
public:
FDVanillaEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps, Size gridPoints,
bool timeDependent = false);
virtual ~FDVanillaEngine() {}
protected:
virtual void setupArguments(
const PricingEngine::arguments*) const;
virtual void setGridLimits() const;
virtual void initializeInitialCondition() const;
virtual void initializeBoundaryConditions() const;
virtual void initializeOperator() const;
shared_ptr<GeneralizedBlackScholesProcess> process_;
Size timeSteps_, gridPoints_;
bool timeDependent_;
mutable Date exerciseDate_;
mutable boost::shared_ptr<Payoff> payoff_;
mutable TridiagonalOperator finiteDifferenceOperator_;
mutable SampledCurve intrinsicValues_;
typedef BoundaryCondition<TridiagonalOperator> bc_type;
mutable std::vector<boost::shared_ptr<bc_type> > BCs_;
virtual void setGridLimits(Real, Time) const;
virtual Time getResidualTime() const;
void ensureStrikeInGrid() const;
private:
Size safeGridPoints(Size gridPoints,
Time residualTime) const;
};This class builds most of the pieces required for a finite-difference
model, based on the data passed to its constructor: a Black-Scholes
process for the underlying, the number of desired time steps and grid
points, and a flag that I’m going to ignore until the next
subsection. Besides the passed inputs, the data members of the class
include information to be retrieved from the instrument (that is, the
exercise date and payoff) and the pieces of the model to be built: the
differential operator, the boundary conditions, and the array of
initial values corresponding to the intrinsic values of the
payoff. The latter array is stored in an instance of the
SampledCurve class, which adds a few utility methods to the stored
data.
The rest of the class interface is made of protected methods that builds and operates on the data members. I’ll just go over them quickly: you can read their implementation in the library for more details.
First, the spectacularly misnamed setupArguments method does the
opposite of its namesake in the Instrument class: it reads the
required exercise and payoff information from the passed arguments
structure and copies them into the corresponding data members of
FDVanillaEngine.
The setGridLimits method determines and stores the minimum and
maximum value of the logarithmic model grid, based on the variance of
the passed process over the residual time of the option. The
calculation enforces that the current value of the underlying is at
the center of the grid, that the strike value is within its range, and
that the number of its points is large enough. (I’d note that the
method might override the number of grid points passed by the user. In
hindsight, I’m not sure that doing it silently is a good idea.) The
actual work is delegated to a number of other methods: an overloaded
version of setGridLimits, safeGridPoints, and
ensureStrikeInGrid.
The initializeInitialCondition method fills the array of intrinsic
values by sampling the payoff on the newly specified grid; thus, it
must be called after the setGridLimits method.
The initializeBoundaryConditions method, to be called as the next
step, instantiates the lower and upper boundary conditions. They’re
both Neumann conditions, and the value of the derivative to be
enforced is calculated numerically from the array of intrinsic values.
Finally, the initializeOperator method creates the tridiagonal
operator based on the calculated grid and the stored process. Again,
the actual work is delegated: in this case, to the OperatorFactory
class, that I’ll describe later.
All of these methods are declared as virtual, so that the default implementations can be overridden if needed. This is not optimal: in order to change any part of the logic one has to use inheritance, which introduces an extra concept just for customization and doesn’t lend itself to different combinations of changes. A Strategy pattern would be better, and would also make some of the logic more reusable by other instruments.
All in all, though, the thing is manageable: see the
FDEuropeanEngine class, shown in the next listing, which can be
implemented in a reasonable amount of code.
template <template <class> class Scheme = CrankNicolson>
class FDEuropeanEngine : public OneAssetOption::engine,
public FDVanillaEngine {
public:
FDEuropeanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false);
private:
mutable SampledCurve prices_;
void calculate() const {
setupArguments(&arguments_);
setGridLimits();
initializeInitialCondition();
initializeOperator();
initializeBoundaryConditions();
FiniteDifferenceModel<Scheme<TridiagonalOperator> >
model(finiteDifferenceOperator_, BCs_);
prices_ = intrinsicValues_;
model.rollback(prices_.values(), getResidualTime(),
0, timeSteps_);
results_.value = prices_.valueAtCenter();
results_.delta = prices_.firstDerivativeAtCenter();
results_.gamma = prices_.secondDerivativeAtCenter();
results_.theta = blackScholesTheta(process_,
results_.value,
results_.delta,
results_.gamma);
}
};Its calculate method sets everything up by calling the appropriate
methods from FDVanillaEngine, creates the model, starts from the
intrinsic value of the option at maturity and rolls it back to the
evaluation date. The value and a couple of Greeks are extracted by the
corresponding methods of the SampledCurve class, and the theta is
calculated from the relationship that the Black-Scholes equation
imposes between it and the other results. (By replacing the
derivatives with the corresponding Greeks, the Black-Scholes equation
says that \( \Theta + \frac{1}{2} \sigma^2 S^2 \Gamma + (r-q)S\Delta
-rV = 0 \).)
What with the figure above then? How do we get three levels of
inheritance between FDVanillaEngine and FDAmericanEngine? It was
due to the desire to reuse whatever pieces of logic we could. As I
said, the idea was correct: there are other options in the library
that use part of this code, such as shout options, or options with
discrete dividends. The architecture could be improved.
First, we have the FDStepConditionEngine, sketched in the following
listing.
template <template <class> class Scheme = CrankNicolson>
class FDStepConditionEngine : public FDVanillaEngine {
public:
FDStepConditionEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps, Size gridPoints,
bool timeDependent = false);
protected:
// ...data members...
virtual void initializeStepCondition() const = 0;
virtual void calculate(PricingEngine::results*) const {
OneAssetOption::results * results =
dynamic_cast<OneAssetOption::results *>(r);
setGridLimits();
initializeInitialCondition();
initializeOperator();
initializeBoundaryConditions();
initializeStepCondition();
typedef /* ... */ model_type;
prices_ = intrinsicValues_;
controlPrices_ = intrinsicValues_;
// ...more setup (operator, BC) for control...
model_type model(operatorSet, bcSet);
model.rollback(arraySet, getResidualTime(),
0.0, timeSteps_, conditionSet);
results->value = prices_.valueAtCenter()
- controlPrices_.valueAtCenter()
+ black.value();
// same for Greeks
}
};It represent a finite-difference engine in which a step condition is
applied at each step of the calculation. In its calculate method,
it implements the bulk of the pricing logic—and then some.
First, it sets up the data members by calling the methods inherited
from FDVanillaEngine, as well as an initializeStepCondition method
that it declares as pure virtual and that derived classes must
implement: it must create an instance of the StepCondition class
appropriate for the given engine. Then, it creates two arrays of
values; the first for the option being priced, and the second for a
European option that will be used as a control variate (this also
requires to set up a corresponding operator, as well as a pricer
object implementing the analytic Black formula). Finally, the model
is created and used for both arrays, with the step condition being
applied only to the first one, and the results are extracted and
corrected for the control variate.
I don’t have particular bones to pick with this class, except for the name, which is far too generic. I’ll just add a note on the usage of control variates. We have already seen the technique in a previous post, where it was used to narrow down the width of the simulated price distribution; here it is used to improve the numerical accuracy. It is currently forced upon the user, since there’s no flag allowing to enable or disable it; and it is relatively more costly than in Monte Carlo simulations (there, the path generation is the bulk of the computation and is shared between the option and the control; here, using it almost doubles the computational effort). The decision of whether it’s worth using should be probably be left to the user. Also, we should use temporary variables for the control data instead of declaring other mutable data members; they’re turning into a bad habit.
Next, the FDAmericanCondition class template, shown in the next
listing.
template <typename baseEngine>
class FDAmericanCondition : public baseEngine {
public:
FDAmericanCondition(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps = 100, Size gridPoints = 100,
bool timeDependent = false);
protected:
void initializeStepCondition() const;
};It takes its base class as a template argument (in our case, it will
be FDVanillaEngine) and provides the initializeStepCondition
method, which returns an instance of the AmericanCondition
class. Unfortunately, the name FDAmericanCondition is quite
confusing: it suggests that the class is a step condition, rather than
a building block for a pricing engine.
The next to last step is the FDEngineAdapter class template.
template <typename base, typename engine>
class FDEngineAdapter : public base, public engine {
public:
FDEngineAdapter(
const shared_ptr<GeneralizedBlackScholesProcess>& p,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false)
: base(p, timeSteps, gridPoints,timeDependent) {
this->registerWith(p);
}
private:
void calculate() const {
base::setupArguments(&(this->arguments_));
base::calculate(&(this->results_));
}
};It connects an implementation and an interface by taking them as
template arguments and inheriting from both: in this case, we’ll have
FDAmericanCondition as the implementation and
OneAssetOption::engine as the interface. The class also provides a
bit of glue code in its calculate method that satisfies the
requirements of the engine interface by calling the methods of the
implementation.
Finally, the FDAmericanEngine class just inherits from
FDEngineAdapter and specifies the classes to be used as bases.
template <template <class> class Scheme = CrankNicolson>
class FDAmericanEngine
: public FDEngineAdapter<
FDAmericanCondition<
FDStepConditionEngine<Scheme> >,
OneAssetOption::engine> {
public:
FDAmericanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false);
};The question is whether it is worth to increase the complexity of the
hierarchy in order to reuse the bits of logic in the base classes. I’m
not sure I have an answer, but I can show an alternate implementation
and let you make the comparison on your own. If we let
FDAmericanEngine inherit directly from FDStepConditionEngine and
OneAssetOption::engine, and if we move into this class the code from
both FDAmericanCondition and FDEngineAdapter (that we can remove
afterwards), we obtain the implementation in the listing below.
template <template <class> class Scheme = CrankNicolson>
class FDAmericanEngine
: public FDStepConditionEngine<Scheme>,
public OneAssetOption::engine {
typedef FDStepConditionEngine<Scheme> fd_engine;
public:
FDAmericanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>& p,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false)
: fd_engine(p, timeSteps, gridPoints, timeDependent) {
this->registerWith(p);
}
protected:
void initializeStepCondition() const;
void calculate() const {
fd_engine::setupArguments(&(this->arguments_));
fd_engine::calculate(&(this->results_));
}
};My personal opinion? I tend to lean towards simplicity in my old
age. The code to be replicated would be little, and the number of
classes that reuse it is not large (about half a dozen in the current
version of the library). Moreover, the classes that we’d remove
(FDAmericanCondition and FDEngineAdapter) don’t really model a
concept in the domain, so I’d let them go without any qualms. Too much
reuse without a proper abstraction might be a thing, after all.
A final note: as you can see, in this framework there are no
high-level classes encapsulating generic model behavior, such as
McSimulation for Monte Carlo (see this post). Whatever
logic we had here was written in classes meant for a specific
instrument—in this case, plain options in a Black-Scholes-Merton
model