Chapter 2, part 2 of 4: Example
Greetings. This is the second in a series of four posts covering chapter 2 of the book; part 1, 3 and 4 can be found here, here and here. I look forward to your comments.
Registration for the next Introduction to QuantLib Development course is still open; it is the course that I teach based on the contents of the Implementing QuantLib blog and book, and you can find more information, a brochure and a booking form by clicking on this link.
Follow me on Twitter if you want to be notified of new posts, or add me to your circles, or subscribe via RSS: the buttons for that are in the footer. Also, make sure to check my Training page, even if you can’t make it to the next course.
Financial instruments and pricing engines
Example: interest-rate swap
In this post, I’ll show how a specific financial instrument can be implemented based on the facilities described in the previous one.
The chosen instrument is the interest-rate swap. As you surely know, it is a contract which consists in exchanging periodic cash flows. The net present value of the instrument is calculated by adding or subtracting the discounted cash-flow amounts depending on whether the cash flows are paid or received.
Not surprisingly, the swap is implemented as a new class deriving from
Instrument. Its outline is shown in listing 2.4. (This
implementation is somewhat outdated. However, it is still used here
since it provides a simpler example.) It contains as data members the
objects needed for the calculations—namely, the cash flows on the
first and second leg and the yield term structure used to discount
their amounts—and two variables used to store additional
results. Furthermore, it declares methods implementing the
Instrument interface and others returning the swap-specific
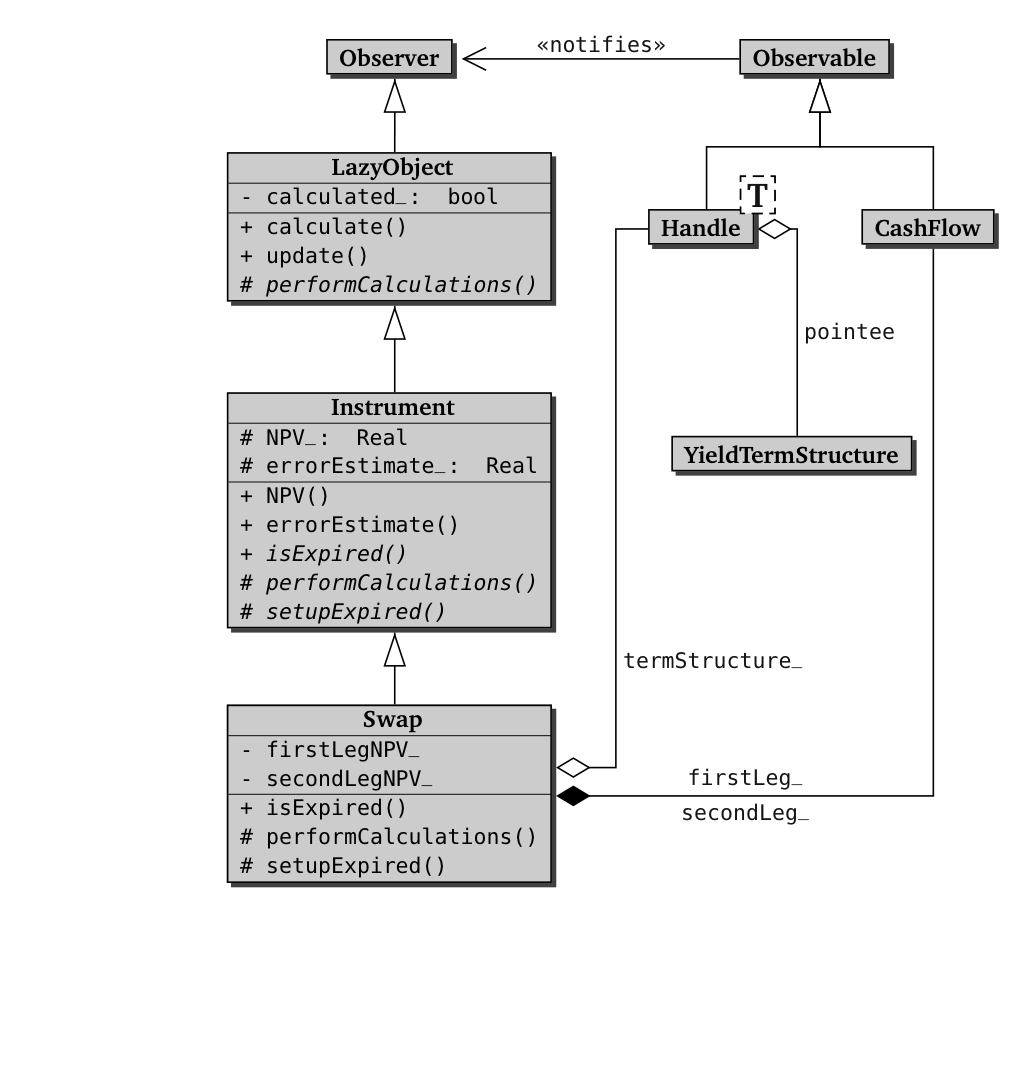
results. The class diagram of Swap and the related classes is shown
in figure 2.1, at the bottom of the post.
Listing 2.4: Partial implementation of the Swap class.
class Swap : public Instrument {
public:
Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure);
bool isExpired() const;
Real firstLegBPS() const;
Real secondLegBPS() const;
protected:
// methods
void setupExpired() const;
void performCalculations() const;
// data members
vector<shared_ptr<CashFlow> > firstLeg_, secondLeg_;
Handle<YieldTermStructure> termStructure_;
mutable Real firstLegBPS_, secondLegBPS_;
};
Swap::Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure)
: firstLeg_(firstLeg), secondLeg_(secondLeg),
termStructure_(termStructure) {
registerWith(termStructure_);
vector<shared_ptr<CashFlow> >::iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
registerWith(*i);
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
registerWith(*i);
}
bool Swap::isExpired() const {
Date settlement = termStructure_->referenceDate();
vector<shared_ptr<CashFlow> >::const_iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
return true;
}
void Swap::setupExpired() const {
Instrument::setupExpired();
firstLegBPS_= secondLegBPS_ = 0.0;
}
void Swap::performCalculations() const {
NPV_ = - Cashflows::npv(firstLeg_,**termStructure_)
+ Cashflows::npv(secondLeg_,**termStructure_);
errorEstimate_ = Null<Real>();
firstLegBPS_ = - Cashflows::bps(firstLeg_, **termStructure_);
secondLegBPS_ = Cashflows::bps(secondLeg_, **termStructure_);
}
Real Swap::firstLegBPS() const {
calculate();
return firstLegBPS_;
}
Real Swap::secondLegBPS() const {
calculate();
return secondLegBPS_;
}The fitting of the class to the Instrument framework is done in
three steps, the third being optional depending on the derived
class. The first step is performed in the class constructor, which
takes as arguments (and copies into the corresponding data members)
the two sequences of cash flows to be exchanged and the yield term
structure to be used for discounting their amounts. The step itself
consists in registering the swap as an observer of both the cash flows
and the term structure. As previously explained, this enables them to
notify the swap and trigger its recalculation each time a change
occurs.
The second step is the implementation of the required interface.
The logic of the isExpired method is simple enough; its body loops
over the stored cash flows checking their payment dates. As soon as it
finds a payment which still has not occurred, it reports the swap as
not expired. If none is found, the instrument has expired. In this
case, the setupExpired method will be called. Its implementation
calls the base-class one, thus taking care of the data members
inherited from Instrument; it then sets to 0 the swap-specific
results.
The last required method is performCalculations. The calculation is
performed by calling two external functions from the Cashflows
class. (If you happen to feel slightly cheated, consider that the
point of this example is to show how to package calculations into a
class—not to show how to implement such calculations. Your curiosity
will be satisfied in a later chapter devoted to cash flows and related
functions.) The first one, namely, npv, is a straightforward
translation of the algorithm outlined above: it cycles on a sequence
of cash flows adding the discounted amount of its future cash
flows. We set the NPV_ variable to the difference of the results
from the two legs. The second one, bps, calculates the basis-point
sensitivity (BPS) of a sequence of cash flows. We call it once per leg
and store the results in the corresponding data members. Since the
result carries no numerical error, the errorEstimate_ variable is
set to Null<Real>()—a specific floating-point value which is used as
a sentinel value indicating an invalid number. (NaN might be a
better choice, but the means of detecting it are not portable. Another
possibility still to be investigated would be to use
boost::optional.)
The third and final step only needs to be performed if—as in this
case—the class defines additional results. It consists in writing
corresponding methods (here, firstLegBPS and secondLegBPS) which
ensure that the calculations are (lazily) performed before returning
the stored results.
The implementation is now complete. Having been written on top of the
Instrument class, the Swap class will benefit from its code. Thus,
it will automatically cache and recalculate results according to
notifications from its inputs—even though no related code was written
in Swap except for the registration calls.
Aside: handles and shared pointers
You might wonder why the Swap constructor accepts the discount curve
as a handle (the smart pointer-to-pointer replacement I mentioned in
the previous post) and the cash flows as simple shared pointers. The
reason is that we might decide to switch to a different curve, which
can be done by means of the handle, whereas the cash flows are part of
the definition of the swap and are thus immutable.
Further developments
You might have noticed a shortcoming in my treatment of the previous
example and of the Instrument class in general. Albeit generic, the
Swap class we implemented cannot manage interest-rate swaps in which
the two legs are paid in different currencies. A similar problem would
arise if the user were to add the values of two instruments whose
values are not in the same currency; the user would have to convert
manually one of the values to the currency of the other before adding
the two.
Such problems stem from a single weakness of the implementation: we
used the Real type (i.e., a simple floating-point number) to
represent the value of an instrument or a cash flow. Therefore, such
results miss the currency information which is attached to them in the
real world.
The weakness might be removed if we were to express such results by
means of the Money class. Instances of such class contain currency
information; moreover, depending on user settings, they are able to
automatically perform conversion to a common currency upon addition or
subtraction.
However, this would be a major change, affecting a large part of the code base in a number of ways. Therefore, it will need some serious thinking before we tackle it (if we do tackle it at all).
Another (and more subtle) shortcoming is that the Swap class fails
to distinguish explicitly between two components of the abstraction it
represents. Namely, there is no clear separation between the data
specifying the contract (the cash-flow specification) and the market
data used to price the instrument (the current discount curve).
The solution is to store in the instrument only the first group of data (i.e., those that would be in its term sheet) and keep the market data elsewhere. (Beside being conceptually clearer, this would prove useful to external functions implementing serialization and deserialization of the instrument—for instance, to and from the FpML format.) The means to do this will be the subject of the next post.
Figure 2.1: Class diagram of the Swap class.